Tập nghiệm của bất phương trình $2x\left( {4 - x} \right)\left( {3 - x} \right)\left( {3 + x} \right) > 0$ là
-
A.
Một khoảng
-
B.
Hợp của hai khoảng.
-
C.
Hợp của ba khoảng.
-
D.
Toàn trục số
- Tìm nghiệm của mỗi nhị thức bậc nhất xuất hiện trong vế trái của bất phương trình.
- Xét dấu vế trái của bất phương trình suy ra tập nghiệm.
Đặt $f\left( x \right) = 2x\left( {4 - x} \right)\left( {3 - x} \right)\left( {3 + x} \right).$
Phương trình $2x = 0 \Leftrightarrow x = 0;\,\,$$4 - x = 0 \Leftrightarrow x = 4;\,\,$
Và $3 - x = 0 \Leftrightarrow x = 3;3 + x = 0 \Leftrightarrow x = - 3$.
Ta có bảng xét dấu:
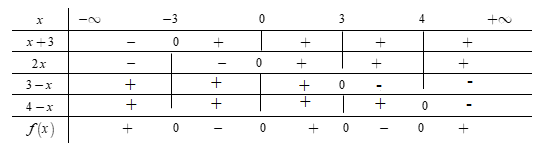
Từ bảng xét dấu ta có $f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x > 4\\0 < x < 3\\x < - \,3\end{array} \right. \Leftrightarrow x \in \left( { - \infty ;\, - 3} \right) \cup \left( {0;\,3} \right) \cup \left( {4;\, + \infty } \right).$
Suy ra tập nghiệm bất phương trình là hợp của ba khoảng.
Đáp án : C
Các bài tập cùng chuyên đề
Cho biểu thức \(f\left( x \right) = \left( {x + 5} \right)\left( {3 - x} \right).\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) \le 0\) là
Cho biểu thức \(f\left( x \right) = \dfrac{1}{{3x - 6}}.\) Tập hợp tất cả các giá trị của \(x\) để \(f\left( x \right) \le 0\) là
Cho biểu thức \(f\left( x \right) = \dfrac{{\left( {x + 3} \right)\left( {2 - x} \right)}}{{x - 1}}.\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) > 0\) là
Cho biểu thức \(f\left( x \right) = \dfrac{{2 - x}}{{x + 1}} + 2.\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) < 0\) là
Tập nghiệm của bất phương trình $\left( {2x + 8} \right)\left( {1 - x} \right) > 0$ có dạng $\left( {a;b} \right).$ Khi đó $b - a$ bằng
Tập nghiệm $S = \left[ {0;5} \right]$ là tập nghiệm của bất phương trình nào sau đây ?
Tích của nghiệm nguyên âm lớn nhất và nghiệm nguyên dương nhỏ nhất của bất phương trình $\left( {3x - 6} \right)\left( {x - 2} \right)\left( {x + 2} \right)\left( {x - 1} \right) > 0$ là
Nghiệm nguyên nhỏ nhất thỏa mãn bất phương trình $\left( {x - 1} \right)\sqrt {x\left( {x + 2} \right)} \ge 0$ là
Bất phương trình $\dfrac{3}{{2 - x}} < 1$ có tập nghiệm là
Tập nghiệm của bất phương trình $\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1$ là
Bất phương trình \(\dfrac{4}{{x - 1}} - \dfrac{2}{{x + 1}} < 0\) có tập nghiệm là
Bất phương trình $\dfrac{1}{{x + 1}} < \dfrac{1}{{{{\left( {x - 1} \right)}^2}}}$ có tập nghiệm \(S\) là
Bất phương trình $\dfrac{{x + 4}}{{{x^2} - 9}} - \dfrac{2}{{x + 3}} < \dfrac{{4x}}{{3x - {x^2}}}$ có nghiệm nguyên lớn nhất là
Nghiệm của bất phương trình $\left| {2x - 3} \right| \le 1$ là
Tập nghiệm của bất phương trình $\left| {x - 3} \right| > - 1$ là
Tập nghiệm của bất phương trình $\left| {5x - 4} \right| \ge 6$ có dạng $S = \left( { - \,\infty ;a} \right] \cup \left[ {b; + \,\infty } \right).$ Tính tổng $P = 5a + b.$
Bất phương trình : $\left| {3x - 3} \right| \le \left| {2x + 1} \right|$ có nghiệm là
Hỏi có bao nhiêu giá trị nguyên $x$ trong $\left[ { - \,2017;2017} \right]$ thỏa mãn bất phương trình \(\left| {2x + 1} \right| < 3x\) ?
Số nghiệm nguyên thỏa mãn bất phương trình $\left| {x + 2} \right| + \left| { - 2x + 1} \right| \le x + 1$ là
Bất phương trình $\left| {x + 2} \right| - \left| {x - 1} \right| < x - \dfrac{3}{2}$ có tập nghiệm là
