Cho biểu thức \(f\left( x \right) = \dfrac{{\left( {x + 3} \right)\left( {2 - x} \right)}}{{x - 1}}.\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) > 0\) là
-
A.
\(x \in \left( { - \,\infty ; - \,3} \right) \cup \left( {1; + \,\infty } \right).\)
-
B.
\(x \in \left( { - \,3;1} \right) \cup \left( {2; + \,\infty } \right).\)
-
C.
\(x \in \left( { - \,3;1} \right) \cup \left( {1;2} \right).\)
-
D.
\(x \in \left( { - \,\infty ; - \,3} \right) \cup \left( {1;2} \right).\)
- Tìm các nghiệm của mỗi nhị thức bậc nhất xuất hiện trong \(f\left( x \right)\).
- Xét dấu các nhị thức bậc nhất và suy ra kết luận.
- Phương trình $x + 3 = 0 \Leftrightarrow x = - \,3;\,\,2 - x = 0 \Leftrightarrow x = 2$ và $x - 1 = 0 \Leftrightarrow x = 1.$
- Bảng xét dấu
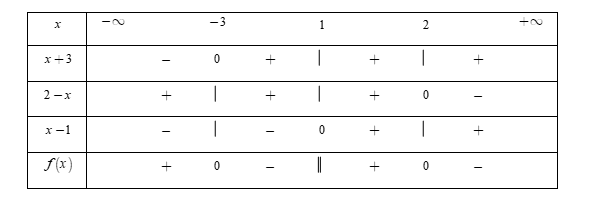
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \,\infty ; - \,3} \right) \cup \left( {1;2} \right).$
Đáp án : D
Đối với dạng xét dấu qua trục số, các em có thể thục hiện:
+) Vẽ trục số, điền các nghiệm theo thứ tự tăng dần trên trục số.
+) Xét dấu trong từng khoảng bằng cách thay từng giá trị của \(x\) thuộc khoảng đang xét và kiểm tra dấu.
Cụ thể: \(f\left( x \right) = \dfrac{{\left( {x + 3} \right)\left( {2 - x} \right)}}{{x - 1}}\)
Các nghiệm: \( - 3;1;2\).

Với \(x > 2\), thay \(x = 3\) được \(f\left( 4 \right) = - 3 < 0\) nên điền dấu \('' - ''\).
Với \(1 < x < 2\) thay \(x = \dfrac{3}{2}\) được \(f\left( {\dfrac{3}{2}} \right) = \dfrac{9}{2} > 0\) nên điền dấu \('' + ''\).
Với \( - 3 < x < 1\) thay \(x = 0\) được \(f\left( 0 \right) = - 6 < 0\) nên điền dấu \('' - ''\).
Với \(x < - 3\) thay \(x = - 4\) được \(f\left( { - 4} \right) = \dfrac{6}{5} > 0\) nên điền dấu \('' + ''\).








Danh sách bình luận