Một ngọn đèn nhỏ \(S\) đặt ở đáy một bể nước \(\left( {n = \frac{4}{3}} \right)\), độ cao mực nước \(h = 60\,\,\left( {cm} \right)\). Bán kính \(r\) bé nhất của tấm gỗ tròn nổi trên mặt nước sao cho không một tia sáng nào từ \(S\) lọt ra ngoài không khí là:

Để không có tia sáng ra ngoài không khí, tia sáng bị phản xạ toàn phần tại mặt phân cách.

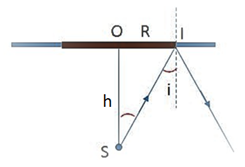
Để xảy ra hiện tượng phản xạ toàn phần, ta có:

\(\sin i \ge \sin {i_{gh}} \Rightarrow \sin i \ge \frac{1}{n}\)

Lại có: \(\sin i = \frac{r}{{\sqrt {{r^2} + {h^2}} }} = \frac{1}{{\sqrt {1 + \frac{{{h^2}}}{{{r^2}}}} }}\)

\(\begin{array}{l} \Rightarrow \frac{1}{{\sqrt {1 + \frac{{{h^2}}}{{{r^2}}}} }} \ge \frac{1}{n} \Rightarrow \sqrt {1 + \frac{{{h^2}}}{{{r^2}}}}  \le n \Rightarrow 1 + \frac{{{h^2}}}{{{r^2}}} \le {n^2} \Rightarrow \frac{{{h^2}}}{{{r^2}}} \le {n^2} - 1\\ \Rightarrow \frac{h}{r} \le \sqrt {{n^2} - 1}  \Rightarrow r \ge \frac{h}{{\sqrt {{n^2} - 1} }} \Rightarrow {r_{\min }} = \frac{h}{{\sqrt {{n^2} - 1} }} = \frac{{60}}{{\sqrt {{{\left( {\frac{4}{3}} \right)}^2} - 1} }} \approx 68\,\,\left( {cm} \right)\end{array}\)