Đề bài
Đề thi THPT QG - 2021 - mã 101
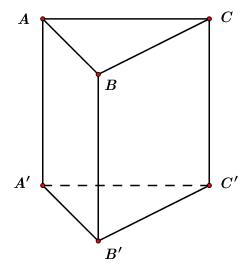
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng \(AA'\) và \(BC'\) bằng
-
A.
\({30^0}\).
-
B.
\({90^0}\).
-
C.
\({45^0}\)
-
D.
\({60^0}\)
Phương pháp giải
Bước 1: Sử dụng định lí: \(\angle \left( {a;b} \right) = \angle \left( {a';b} \right)\) với \(a'//a\).
Bước 2: Sử dụng tính chất của tam giác vuông cân để tính góc.
Lời giải của GV Loigiaihay.com
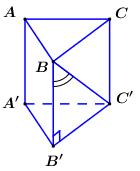
Bước 1:
Do \(AA'//BB' \Rightarrow \angle \left( {AA';BC'} \right) \)\(= d\left( {BB';BC'} \right) = \angle B'BC\).
Bước 2:
Xét \(\Delta B'BC\) vuông tại \(B'\) có: \(BB' = B'C' = a\).
\( \Rightarrow \Delta B'BC\) vuông cân tại \(B' \Rightarrow \angle B'BC = {45^0}\).
Đáp án : C
