Đề thi THPT QG - 2021 - mã 101
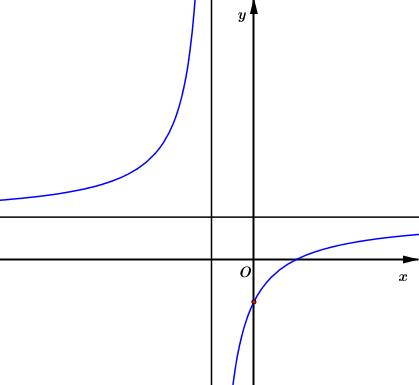
Biết hàm số \(y = \dfrac{{x + a}}{{x + 1}}\,\,(a\) là số thực cho trước, \(a \ne 1\)) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
-
A.
\(y' < 0,\,\,\forall x \ne - 1\).
-
B.
\(y' > 0,\,\,\forall x \ne - 1\).
-
C.
\(y' < 0,\,\,\forall x \in \mathbb{R}\).
-
D.
\(y' > 0,\,\,\forall x \in \mathbb{R}\).
Dựa vào chiều biến thiên và tập xác định của hàm số.
+ Từ đồ thị ta nhận thấy hàm số đồng biến trên mỗi khoảng xác định \( \Rightarrow y' > 0\).
+ Do hàm số \(y = \dfrac{{x + a}}{{x + 1}}\) không xác định tại \(x = - 1\) \( \Rightarrow y' > 0\,\,\forall x \ne - 1\).
Đáp án : B
Các bài tập cùng chuyên đề
Hàm số nào dưới đây có tập xác định bằng \(\mathbb{R}\)?
Hàm số \(y = \dfrac{{3x - 6}}{{x - 2}}\) xác định khi:
Hàm số nào dưới đây không có cực trị?
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) với \(ad - bc \ne 0\) là:
Cho hàm số \(y = \dfrac{{x - 3}}{{2x - 6}}\), chọn kết luận đúng:
Giao điểm của hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) được gọi là:
Giao điểm hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ - x + 1}}{{2x - 3}}\) là:
Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có đồ thị như hình bên thì:
Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có bảng biến thiên như hình vẽ thì:
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
Bảng biến thiên trên là bảng biến thiên của đồ thị hàm số nào?
Hàm số nào dưới đây có thể có bảng biến thiên như hình vẽ?
Cho hàm số \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
Khẳng định nào dưới đây đúng?
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:
Chọn kết luận đúng:
Cho hàm số \(y = \dfrac{{3x + 1}}{{x + 2}}\left( C \right).\) Các đường tiệm cận của (C) cùng với 2 trục tọa độ tạo thành hình chữ nhật có diện tích bằng:
Cho hàm số \(y = \dfrac{{x + b}}{{cx - 1}}\) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
Cho hàm số \(y = f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) với \(a,\,\,b,\,\,c,\,\,d \in \mathbb{R}\), \(c \ne 0\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Biết rằng giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) bằng \(3\). Giá trị của \(f\left( { - 2} \right)\) bằng:
