Một hình chóp tứ giác đều có chiều cao $35\,cm$ , cạnh đáy $24\,cm$ .

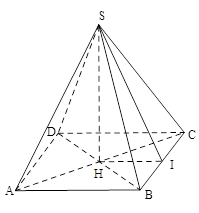
Xét hình chóp tứ giác đều $S.ABCD$ có đường cao

$SH = 35cm$, cạnh $AB = 24cm\,\,$

Gọi $SI$  là đường cao của $\Delta SBC$. Tam giác $SBC$ cân tại $S$  nên $BI = IC$ . Ta có $HI$  là đương trung bình của $\Delta ABC$nên $HI = \dfrac{{AB}}{2} = \dfrac{{24}}{2} = 12\left( {cm} \right)$

Áp dụng định lí Py-ta-go vào tam giác vuông $SHI$ Ta có $S{I^2} = S{H^2} + H{I^2} = {35^2} + {12^2} = 1369 = {37^2}$

Nên $SI = 37\left( {cm} \right)$.

Chu vi đáy bằng $24.4 = 96\left( {cm} \right)$

${S_{xq}} = p.d = \dfrac{{96}}{2}.37 = 1776\left( {c{m^2}} \right)$

Diện tích đáy bằng $24.24 = 576\left( {c{m^2}} \right)$

Diện tích toàn phần $1776 + 576 = 2352\left( {c{m^2}} \right)$