Đề bài
Cho các tập hợp \(A = \left( { - \infty ;m} \right)\) và \(B = \left[ {3m - 1;3m + 3} \right]\). Tìm \(m\) để \({C_\mathbb{R}}A \cap B \ne \emptyset \)
-
A.
\(m > - \dfrac{3}{2}\)
-
B.
\(m \le - \dfrac{3}{2}\)
-
C.
\(m \ge - \dfrac{3}{2}\)
-
D.
\(m < - \dfrac{3}{2}\)
Phương pháp giải
+) Tìm \({C_\mathbb{R}}A\).
+) Để \({C_\mathbb{R}}A \cap B \ne \emptyset \) thì chúng phải có ít nhất 1 điểm chung.
Lời giải của GV Loigiaihay.com
Ta có: \({C_\mathbb{R}}A = \left[ {m; + \infty } \right)\)
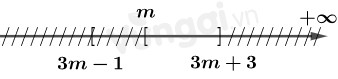
\( \Rightarrow {C_\mathbb{R}}A \cap B \ne \emptyset \)\(\Leftrightarrow m \le 3m + 3 \Leftrightarrow m \ge - \dfrac{3}{2}.\)
Vậy \(m \ge - \dfrac{3}{2}\) là giá trị cần tìm.
Đáp án : C
