Cho lăng trụ đứng có kích thước như hình vẽ.
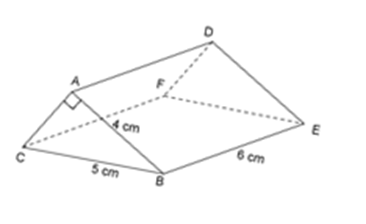
Số nào trong các số sau đây là thể tích của hình lăng trụ đứng đó?
-
A.
$20\,c{m^3}$
-
B.
$36\,c{m^3}$
-
C.
$26\,c{m^3}$
-
D.
$9\,c{m^3}$
Vận dụng kiến thức về định lý Py-ta-go và các công thức tính diện tích, thể tích hình lăng trụ đứng để giải bài toán
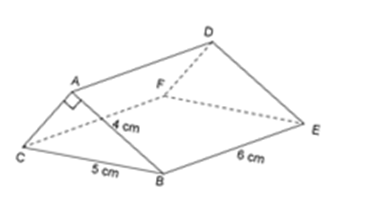
Hình lăng trụ đứng đã cho có đáy là một tam giác vuông.
Áp dụng định lý Pytago cho tam giác vuông $ABC$ , ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2} \Leftrightarrow {4^2} + A{C^2} = {5^2}\\ \Leftrightarrow A{C^2} = {5^2} - {4^2} = 9 \Rightarrow AC = 3\;cm.\end{array}\)
Vậy diện tích đáy của hình lăng trụ đứng là: \(S = {S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.4 = 6\;c{m^2}\)
Vậy thể tích của hình lăng trụ đứng là: \(V = S.h = S.BE = 6.6 = 36\;c{m^3}\)
Đáp án : B
- Học sinh cần nắm vững kiến thức về hình lăng trụ đứng.
- Khi áp dụng định lý Pitago, cần xác định đúng cạnh huyền, cạnh góc vuông
của tam giác vuông để viết biểu thức chính xác.








Danh sách bình luận