Đề bài
Tính thể tích của một hình lập phương, biết rằng đường chéo của hình lập phương bằng $\sqrt {12} cm$.
-
A.
$8\,c{m^3}$
-
B.
$4\,c{m^3}$
-
C.
$16\,c{m^2}$
-
D.
$18\,c{m^3}$
Phương pháp giải
+ Từ các điều kiện đề bài tìm cạnh của hình lập phương.
+ Sử dụng công thức thể tích hình lập phương để tính toán.
Lời giải của GV Loigiaihay.com
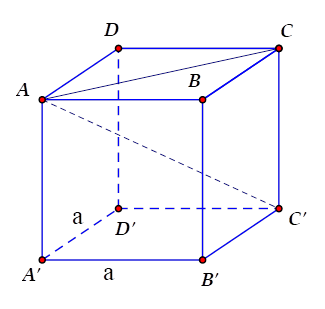
Gọi $a$ là cạnh của hình lập phương. Theo định lý Pitago ta có $AC^2=AB^2+BC^2=a^2+a^2$ suy ra $AC^2+CC'^2$\(={a^2} + {a^2} + {a^2} \)\(=A{C'^2} = {\left( {\sqrt {12} } \right)^2} = 12\)
Từ đó $a = 2\left( {cm} \right).$ Thể tích của hình lập phương bằng \(2^3=8\left( {c{m^3}} \right)\) .
Đáp án : A
