Cho tam giác ABC có AM là đường trung tuyến, N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC. Chọn khẳng định đúng nhất.
-
A.
\(DE{\rm{//}}BC\)
-
B.
\(\dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{CE}}\)
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai\(\)
Bước 1: Vẽ thêm đường thẳng song song để hình thành các cặp đoạn thẳng tỉ lệ.
Bước 2: Áp dụng định lý Talet và tính chất bắc cầu để tìm ra tỉ lệ thức cần chứng minh
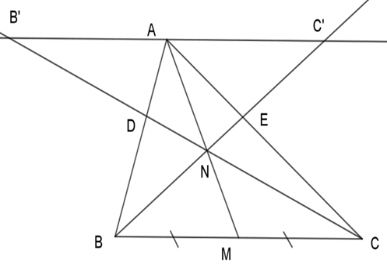
Kẻ đường thẳng đi qua $A$ song song với $BC$ lần lượt cắt $CD$ và $BE$ kéo dài tại \(B'\) và \(C'\).
Vì M là trung điểm của $BC$ nên \(BM = MC\).
Vì \(AB'{\rm{//}}MC\), áp dụng định lý Talet ta có:
\(\dfrac{{AN}}{{NM}} = \dfrac{{AB'}}{{MC}}\) (1)\(\)
Vì \(AC'{\rm{//}}\,BM\), áp dụng định lý Talet ta có:
\(\dfrac{{AN}}{{NM}} = \dfrac{{AC'}}{{BM}}\) (2)
Từ (1) và (2) ta có: \(\dfrac{{AB'}}{{MC}} = \dfrac{{AC'}}{{BM}}\)
Ta có $M$ là trung điểm của $BC$ \( \Rightarrow \)\(BM = MC\)\( \Rightarrow \)\(AB' = AC'\) (*)
Vì \(AB'{\rm{//}}\,BC\), áp dụng định lý Talet ta có:
\(\dfrac{{AD}}{{DB}} = \dfrac{{AB'}}{{BC}}\) (**)
Vì \(AC'{\rm{//}}\,BC\), áp dụng định lý Talet ta có:
\(\dfrac{{AE}}{{EC}} = \dfrac{{AC'}}{{BC}}\) (***)
Từ (*), (**) và (***) ta có:
\(\dfrac{{AD}}{{DB}} = \dfrac{{AB'}}{{BC}} = \dfrac{{AE}}{{EC}} = \dfrac{{AC'}}{{BC}}\)
\( \Rightarrow \dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}}\)\( \Leftrightarrow \dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{CE}}\) hay \(DE{\rm{//}}BC\)
Đáp án : C
Các bài tập cùng chuyên đề
Viết tỉ số cặp đoạn thẳng có độ dài như sau: $AB = 4\,dm,CD = 20\,dm$
Hãy chọn câu sai. Cho hình vẽ với $AB<AC$:
Cho hình vẽ, trong đó $DE{\rm{//}}BC$, $AD = 12,\,\,DB = 18,\,\,CE = 30$. Độ dài $AC$ bằng:
Chọn câu trả lời đúng:
Cho hình thang $ABCD$ ($AB{\rm{//}}CD$),$O$ là giao điểm của $AC$ và$BD$ . Xét các khẳng định sau:
(I) \(\dfrac{{OA}}{{OC}} = \dfrac{{AB}}{{CD}}\) (II) \(\dfrac{{OB}}{{OC}} = \dfrac{{BC}}{{AD}}\)
Cho biết $M$ thuộc đoạn thẳng $AB$ thỏa mãn \(\dfrac{{AM}}{{MB}} = \dfrac{3}{8}\). Tính tỉ số \(\dfrac{{AM}}{{AB}}\) ?
Cho hình vẽ, trong đó \(AB{\rm{//}}CD\) và \(DE = EC\). Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
(I) \(\dfrac{{AK}}{{EC}} = \dfrac{{KB}}{{DE}}\) (II)\(AK = KB\)
(III) \(\dfrac{{AO}}{{AC}} = \dfrac{{AB}}{{DC}}\) (IV) \(\dfrac{{AK}}{{EC}} = \dfrac{{OB}}{{OD}}\)
Chọn câu trả lời đúng: Cho hình bên, biết \(DE{\rm{//}}AC\), tìm \(x\) :
Cho tam giác $ABC$ có $AB = 9\,cm$, điểm $D$ thuộc cạnh $AB$ sao cho $AD = 6\,cm$. Kẻ $DE$ song song với $BC$ $\left( {E \in AC} \right)$, kẻ $EF$ song song với $CD$ $\left( {F \in AB} \right)$. Tính độ dài $AF$ .
Tính các độ dài $x,y$ trong hình bên:
Tìm giá trị của \(x\) trên hình vẽ.
Cho hình thang $ABCD$ $\left( {AB{\rm{//}}CD} \right)$ có $BC = 15\,cm$. Điểm $E$ thuộc cạnh $AD$ sao cho $\dfrac{{AE}}{{AD}} = \dfrac{1}{3}$. Qua $E$ kẻ đường thẳng song song với $CD$ , cắt $BC$ ở $F$ . Tính độ dài $BF$ .
Cho tam giác $ABC$ . Một đường thẳng song song với $BC$ cắt các cạnh $AB$ và $AC$ theo thứ tự ở $D$ và $E$ . Chọn câu đúng.
Cho tam giác $ABC$ , đường trung tuyến $AD$ . Gọi $K$ là điểm thuộc đoạn thẳng $AD$ sao cho $\dfrac{{AK}}{{KD}} = \dfrac{1}{2}$. Gọi $E$ là giao điểm của $BK$ và $AC$ . Tính tỉ số $\dfrac{{AE}}{{EC}}$.
Cho hình thang \(ABCD\)\(\left( {AB//CD} \right)\) có diện tích \(36\,c{m^2}\),\(AB = 4\,{\rm{cm,CD = 8}}\,{\rm{cm}}\). Gọi \(O\) là giao điểm của hai đường chéo. Tính diện tích tam giác \(COD\).
Cho tứ giác \(ABCD\), lấy bất kỳ \(E \in BD\) . Qua \(E\) vẽ \(EF\) song song với \(AD\)( \(F\) thuộc \(AB\)), vẽ \(EG\) song song với \(DC\)(\(G\) thuộc\(BC\)). Chọn khẳng định sai.
Cho tam giác ABC, M thuộc cạnh AB, N thuộc cạnh BC, biết \(\frac{{MA}}{{MB}} = \frac{{NC}}{{NB}} = \frac{2}{5},MN = 15\left( {cm} \right)\). Tính độ dài cạnh AC.
