Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Cho biết $BH = 4cm,CH = 9cm$. Gọi $D,E$ lần lượt là hình chiếu vuông góc của $H$ trên các cạnh $AB$ và $AC$. Các đường thẳng vuông góc với $DE$ tại $D$ và $E$ lần lượt cắt $BC$ tại $M,N$ . (hình vẽ)
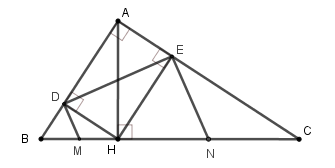
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Cho biết $BH = 4cm,CH = 9cm$. Gọi $D,E$ lần lượt là hình chiếu vuông góc của $H$ trên các cạnh $AB$ và $AC$. Các đường thẳng vuông góc với $DE$ tại $D$ và $E$ lần lượt cắt $BC$ tại $M,N$ . (hình vẽ)

Tính diện tích tứ giác $DENM$
Tính diện tích tứ giác $DENM$
\({S_{DENM}} = 19,5\,c{m^2}\)
\({S_{DENM}} = 20,5\,c{m^2}\)
\({S_{DENM}} = 19\,c{m^2}\)
\({S_{DENM}} = 21,5\,c{m^2}\)
Đáp án: A
Bước 1 : Chứng minh $DENM$ là hình thang vuông
Bước 2: Sử dụng công thức tính diện tích hình thang .
Vì $DM \bot DE;$$EN \bot DE \Rightarrow DM{\rm{//}}EN;$$\widehat D = \widehat E = 90^\circ $ nên $DENM$ là hình thang vuông
Theo kết quả hai câu trước ta có: $DM = \dfrac{{BH}}{2} = 2;$$EN = \dfrac{{CH}}{2} = 4,5;DE = 6$
Nên ${S_{DENM}} = \dfrac{{\left( {DM + EN} \right).DE}}{2} $$= 19,5\,c{m^2}$

Tính độ dài đoạn thẳng $DE$.
Tính độ dài đoạn thẳng $DE$.
$DE = 5\,cm$
$DE = 8\,cm$
$DE = 7\,cm$
$DE = 6\,cm$
Đáp án: D
Bước 1: Chứng minh $DE = AH$
Bước 2: Sử dụng hệ thức $A{H^2} = BH.CH$ từ đó tính $AH$$ \Rightarrow DE$.
Tứ giác $AEHD$ là hình chữ nhật vì $\widehat A = \widehat E = \widehat D = 90^\circ $ nên $DE = AH$
Xét $\Delta ABC$ vuông tại $A$ có $A{H^2} = HB.HC$$ = 4.9 = 36 \Rightarrow AH = 6$
Nên $DE = 6\,cm$.
Kết luận nào sau đây là đúng?
Kết luận nào sau đây là đúng?
\(MN = \dfrac{1}{3}BC\)
\(MN = \dfrac{1}{2}BC\)
\(MN = \dfrac{3}{4}BC\)
\(MN = \dfrac{2}{3}BC\)
Đáp án: B
Chứng minh $M$ là trung điểm của $BH$, $N$ là trung điểm của $CH$
+) Ta có $\widehat {NEC} + \widehat {AED} = 90^\circ $ mà $\widehat {AED} = \widehat {HAE}$ (do $AEHD$ là hình chữ nhật) và $\widehat {HAE} = \widehat {ABC}$ (cùng phụ với $\widehat {ACB}$) nên $\widehat {NEC} + \widehat {ABC} = 90^\circ $ mà $\widehat {ACB} + \widehat {ABC} = 90^\circ $ nên $\widehat {ACB} = \widehat {NEC}$ hay $\Delta NEC$ cân tại $N$$ \Rightarrow EN = NC$.$\left( 1 \right)$
+) $\widehat {NEC} + \widehat {HEN} = 90^\circ $ mà $\widehat {NEC} = \widehat {NCE} \Rightarrow \widehat {NCE} + \widehat {HEN} = 90^\circ $, lại có $\widehat {NCE} + \widehat {NHE} = 90^\circ $ nên $\widehat {NEH} = \widehat {NHE}$ hay $\Delta NEH$ cân tại $N$ suy ra $NE = NH$, $\left( 2 \right)$
Từ $\left( 1 \right);\left( 2 \right)$ ta có $NH = NC$
Tương tự ta có $MH = MB$ nên $MN = MH + NH = \dfrac{1}{2}HB + \dfrac{1}{2}HC = \dfrac{1}{2}BC$.







