Bắn hạt prôtôn có động năng 5,5 MeV vào hạt nhân \(_3^7Li\) đang đứng yên, gây ra phản ứng hạt nhân \(p + {}_3^7Li \to 2\alpha \). Giả sử phản ứng không kèm theo bức xạ γ, hai hạt α có cùng động năng và bay theo hai hướng tạo với nhau góc 160⁰. Coi khối lượng của mỗi hạt tính theo đơn vị u gần đúng bằng số khối của nó. Năng lượng mà phản ứng tỏa ra là

Phương trình phản ứng hạt nhân: \({}_1^1p + {}_3^7Li \to 2{}_2^4He\)

Năng lượng toả ra của phản ứng: Q = 2K_α – K_p

K_p = 5,5 MeV

Định luật bảo toàn động lượng: \(\overrightarrow {{p_p}}  = \overrightarrow {{p_{\alpha 1}}}  + \overrightarrow {{p_{\alpha 2}}} \)

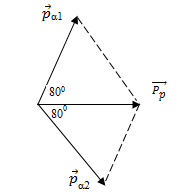
Áp dụng định lí hàm số cos ta có:

\(\eqalign{
& p_p^2 = p_\alpha ^2 + p_\alpha ^2 + 2p_\alpha ^2.c{\rm{os}}{160^0} \Leftrightarrow p_p^2 = 2p_\alpha ^2(1 + c{\rm{os}}{160^0}) \Leftrightarrow 2{m_p}{K_p} = 2.2{m_\alpha }{K_\alpha }(1 + c{\rm{os}}{160^0}) \cr
& \Leftrightarrow {K_p} = 2.4.{K_\alpha }(1 + c{\rm{os}}{160^0}) \Rightarrow {K_\alpha } = {{{K_p}} \over {8(1 + c{\rm{os}}{{160}^0})}} = 11,4(MeV) \cr} \)

 => Năng lượng toả ra của phản ứng: Q = 17,3 (MeV)