Cho đoạn thẳng \(MN = 6cm\). Vẽ đường tròn \(\left( {M;4,5cm} \right)\) và \(\left( {N;3,5cm} \right)\). Hai đường tròn tâm \(M;N\) lần lượt cắt đoạn thẳng \(MN\) tại \(K;I\).
Cho đoạn thẳng \(MN = 6cm\). Vẽ đường tròn \(\left( {M;4,5cm} \right)\) và \(\left( {N;3,5cm} \right)\). Hai đường tròn tâm \(M;N\) lần lượt cắt đoạn thẳng \(MN\) tại \(K;I\).
Tính độ dài \(NK\).
Tính độ dài \(NK\).
\(NK = 2,5cm\)
\(NK = 1cm\)
\(NK = 3,5cm\)
\(NK = 1,5cm\)
Đáp án: D
+ Tính \(MK\)
+ Chứng minh \(K\) nằm giữa hai điểm \(M;N\)
+ Tính \(NK\) dựa vào công thức cộng đoạn thẳng
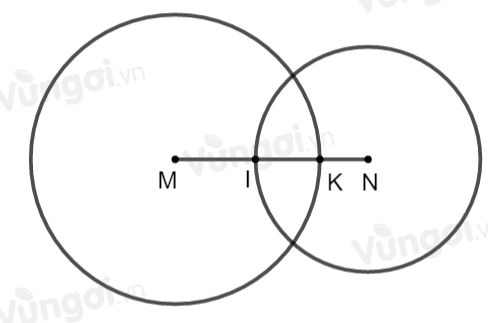
Vì \(K\) thuộc \(\left( {M;4,5cm} \right)\) nên \(MK = 4,5cm\)
Vì \(MK < MN\,\left( {4,5cm < 6cm} \right)\) nên điểm \(K\) nằm giữa hai điểm \(M;N\)
Do đó \(MK + KN = MN \Rightarrow KN = MN - MK\) \( = 6 - 4,5 = 1,5cm\).
Vậy \(NK = 1,5cm\).
Chọn câu đúng.
Chọn câu đúng.
Điểm \(I\) là trung điểm của đoạn thẳng \(MN\)
\(MI < NK\)
\(MI > NK\)
\(MI = 1,5\,cm\)
Đáp án: C
+ Tính \(NI\) và \(MI\), từ đó suy ra đáp án đúng.
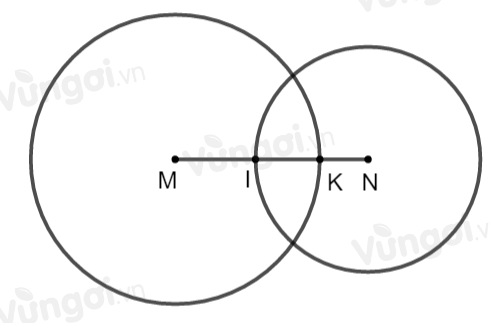
Vì \(I\) thuộc \(\left( {N;3,5cm} \right)\) nên \(NI = 3,5cm (1)\)
Vì \(NI < NM\left( {3,5cm < 6cm} \right)\) nên điểm \(I\) nằm giữa hai điểm \(M;N\)
Do đó \(NI + IM = NM \Rightarrow IM = NM - NI\) \( = 6 - 3,5 = 2,5cm (2)\).
Từ \((1);(2)\) suy ra \(NI \ne MI\,\) nên \(I\) không là trung điểm của đoạn thẳng \(MN\). Vậy A sai, D sai
Theo câu trước ta có \(NK = 1,5cm\) nên \(MI > NK(do\,\,2,5\,cm > 1,5\,cm)\). Vậy B sai, C đúng
