Trong mặt phẳng Oxy, cho tam giác \(ABC\) cân, cạnh đáy \(BC:\) \(x + 3y + 1 = 0,\) cạnh bên \(AB:\) \(x - y + 5 = 0;\) đường thẳng chứa \(AC\) đi qua \(M\left( { - 4; - 1} \right)\). Tìm tọa độ đỉnh \(C\).
Viết phương trình đường thẳng các đường đi qua điểm C.
Đường thẳng d đi qua \(M\left( { - 4; - 1} \right)\) và \(d//BC\) nên d có VTPT \(\overrightarrow {{n_d}} = \overrightarrow {{n_{BC}}} = \left( {1;3} \right)\). Đường thẳng d có phương trình: \(1\left( {x + 4} \right) + 3\left( {y + 1} \right) = 0 \Leftrightarrow x + 3y + 7 = 0\).
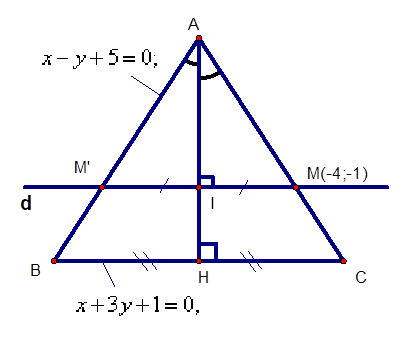
Gọi \(M' = d \cap AB.\) Tọa độ M’ là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x + 3y + 7 = 0\\x - y + 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{{11}}{2}\\y = - \frac{1}{2}\end{array} \right. \Rightarrow M'\left( { - \frac{{11}}{2}; - \frac{1}{2}} \right).\)
I là trung điểm của MM’. Suy ra: \(I\left( { - \frac{{19}}{4}; - \frac{3}{4}} \right).\)
Đường cao AH đi qua I và vuông góc với BC nên có VTPT \(\overrightarrow {{n_{AH}}} = \overrightarrow {{u_{BC}}} = \left( {3; - 1} \right).\) AH có phương trình: \(3\left( {x + \frac{{19}}{4}} \right) - 1\left( {y + \frac{3}{4}} \right) = 0 \Leftrightarrow 6x - 2y + 27 = 0.\)
Cách 1. \(H = AH \cap BC \Rightarrow \)tọa độ H là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}6x - 2y + 27 = 0\\x + 3y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{{83}}{{20}}\\y = \frac{{21}}{{20}}\end{array} \right. \Rightarrow H\left( { - \frac{{83}}{{20}};\frac{{21}}{{20}}} \right).\)
H là trung điểm của BC nên \(C\left( { - \frac{{43}}{{10}};\frac{{11}}{{10}}} \right).\)
Cách 2.
Ta có: \(A = AH \cap AB\). Tọa độ A là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}6x - 2y + 27 = 0\\x - y + 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{{17}}{4}\\y = \frac{3}{4}\end{array} \right. \Rightarrow A\left( { - \frac{{17}}{4};\frac{3}{4}} \right).\)
AC đi qua M(- 4; - 1) và nhận \(\overrightarrow {AM} = \left( {\frac{1}{4}; - \frac{7}{4}} \right)\) làm VTCP, do đó AC có VTPT \(\overrightarrow {{n_{AC}}} = \left( {7;1} \right).\) AC có phương trình: \(7\left( {x + 4} \right) + 1\left( {y + 1} \right) = 0 \Leftrightarrow 7x + y + 29 = 0.\)
\(C = AC \cap BC \Rightarrow C\left( {\frac{{ - 43}}{{10}};\frac{{11}}{{10}}} \right).\)








Danh sách bình luận