Một con lắc lò xo có độ cứng k = 100 N/m, đầu trên cố định còn đầu dưới gắn vật nặng \(m = 0,4kg\). Cho vật m dao động điều hòa theo phương thẳng đứng thì thấy thời gian lò xo nén trong một chu kì là \(0,1s\). Cho \(g=10m/s^2= {\pi}^2m/s^2\). Biên độ dao động của vật là:
-
A.
\(8\sqrt 3 cm\)
-
B.
\(4cm\)
-
C.
\(4\sqrt 2 cm\)
-
D.
\(4\sqrt 3 cm\)
+ Sử dụng công thức tính độ dãn của lò xo ở VTCB: \(\Delta l = \dfrac{{mg}}{k}\)
+ Sử dụng công thức tính chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{m}{k}} \)
+ Vận dụng tỉ số thời gian nén trên chu kì => tỉ lệ => Biên độ
Ta có:
Độ dãn của lò xo ở VTCB: \(\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,4.10}}{{100}} = 0,04m = 4cm\)
Chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{m}{k}} = 2\pi \sqrt {\dfrac{{0,4}}{{100}}} = 0,4{\rm{s}}\)
\(\dfrac{{{t_n}}}{T} = \dfrac{{0,1}}{{0,4}} = \dfrac{1}{4} \to {t_n} = \dfrac{T}{4}\)
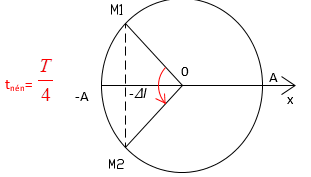
=> \(\Delta l = \dfrac{A}{{\sqrt 2 }} \to A = \sqrt 2 \Delta l = 4\sqrt 2 cm\)
Đáp án : C








Danh sách bình luận