Đề bài
Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E, F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I, J, K thẳng hàng.
Phương pháp giải
Nếu hai mặt phân biệt (P) và (Q) có điểm chung thì chúng có một đường thẳng chung duy nhất d chứa tất cả các điểm chung của hai mặt phẳng đó. Đường thẳng d đó gọi là giao tuyến của hai mặt phẳng (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\).
Lời giải của GV Loigiaihay.com
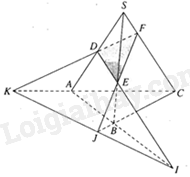
Trong mặt phẳng (SAB), I là giao điểm của DE và AB.
Ta có: \(I \in DE \subset \left( {DEF} \right),I \in AB \subset \left( {ABC} \right)\).
Lí luận tương tự ta có J, K đều thuộc hai mặt phẳng (ABC) và mặt phẳng (DEF).
Do đó, 3 điểm I, J, K đều thuộc giao tuyến của hai mặt phẳng (ABC) và mặt phẳng (DEF).
Do đó, 3 điểm I, J, K thẳng hàng.
Xem thêm : Đề thi, đề kiểm tra Toán lớp 11 - Cánh diều
