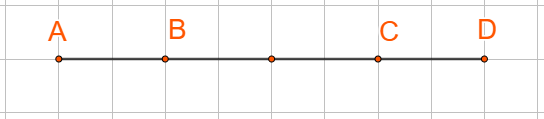
Ở hình 61, tìm k trong mỗi trường hợp sau:
a) \(\overrightarrow {AC} = k.\overrightarrow {AD} \)
b) \(\overrightarrow {BD} = k.\overrightarrow {DC} \)
Từ hình vẽ suy ra hướng và tỉ số độ dài của hai vecto.
a) Ta có: \(\overrightarrow {AC} ,\overrightarrow {AD} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AC} } \right| = \frac{3}{4}\left| {\overrightarrow {AD} } \right|\)
Suy ra \(\overrightarrow {AC} = \frac{3}{4}\overrightarrow {AD} .\) Vậy \(k = \frac{3}{4}.\)
b) Ta có: \(\overrightarrow {BD} ,\overrightarrow {DC} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {BD} } \right| = 3\left| {\overrightarrow {DC} } \right|\)
Suy ra \(\overrightarrow {BD} = - 3\overrightarrow {DC} .\) Vậy \(k = - 3.\)

Các bài tập cùng chuyên đề
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương khác \(\overrightarrow 0 \) và cho \(\overrightarrow c = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b \). So sánh độ dài và hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)
Cho \(\overrightarrow a \ne \overrightarrow 0 \). Khẳng định nào sau đây là sai?
A. \(\overrightarrow a \) và \(4\overrightarrow a \) cùng phương
B. \(\overrightarrow a \) và \( - 4\overrightarrow a \) cùng phương
C. \(\overrightarrow a \) và \(4\overrightarrow a \) không cùng hướng
D. \(\overrightarrow a \) và \( - 4\overrightarrow a \) ngược hướng