Cho hình chóp S.ABC. Bên trong tam giác ABC ta lấy một điểm O bất kỳ. Từ O ta dựng các đường thẳng lần lượt song song với SA, SB, SC và cắt các mặt phẳng (SBC), (SCA), (SAB) theo thứ tự tại \({A'},{B'},{C'}\). Khi đó \(T = \frac{{OA'}}{{SA}} + \frac{{OB'}}{{SB}} + \frac{{OC'}}{{SC}}\) bằng bao nhiêu?
-
A.
\(\frac{1}{3}\)
-
B.
\(\frac{1}{2}\)
-
C.
\(\frac{3}{4}\)
-
D.
\(1\)
Vẽ hình, tìm giao điểm của đường thẳng với mặt phẳng và sử dụng định lý Ta ˗ lét để chứng minh.
Định lý Ta lét: Nếu một đường thẳng cắt 2 cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ững tỉ lệ thì nó song song với cạnh còn lại của tam giác.
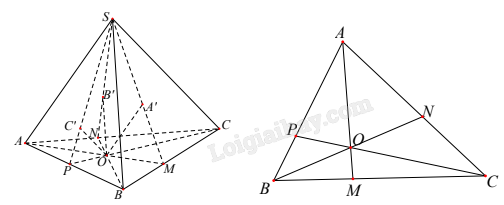
Gọi \(M = AO \cap BC;N = AO \cap BC;P = CO \cap AB\).
Ta có \(\frac{{OA'}}{{SA}} = \frac{{MO}}{{MA}} = \frac{{{S_{CMO}}}}{{{S_{CMA}}}} = \frac{{{S_{BMO}}}}{{{S_{BMA}}}} = \frac{{{S_{CMO}} + {S_{BMO}}}}{{{S_{CMA}} + {S_{BMA}}}} = \frac{{{S_{OBC}}}}{{{S_{ABC}}}}\);
\(\frac{{OB'}}{{SB}} = \frac{{NO}}{{NB}} = \frac{{{S_{ANO}}}}{{{S_{ANB}}}} = \frac{{{S_{CNO}}}}{{{S_{CNB}}}} = \frac{{{S_{ANO}} + {S_{CNO}}}}{{{S_{ANB}} + {S_{CNB}}}} = \frac{{{S_{OAC}}}}{{{S_{ABC}}}}\);
\(\frac{{OC'}}{{SC}} = \frac{{PO}}{{PC}} = \frac{{{S_{APO}}}}{{{S_{APC}}}} = \frac{{{S_{BPO}}}}{{{S_{BPC}}}} = \frac{{{S_{APO}} + {S_{BPO}}}}{{{S_{APC}} + {S_{BPC}}}} = \frac{{{S_{OAB}}}}{{{S_{ABC}}}}\).
\( \Rightarrow T = \frac{{OA'}}{{SA}} + \frac{{OB'}}{{SB}} + \frac{{OC'}}{{SC}} = \frac{{{S_{OBC}}}}{{{S_{ABC}}}} + \frac{{{S_{OAC}}}}{{{S_{ABC}}}} + \frac{{{S_{OAB}}}}{{{S_{ABC}}}} = \frac{{{S_{ABC}}}}{{{S_{ABC}}}} = 1\).
* Bài toán phụ: Chứng minh \(\frac{{MO}}{{MA}} = \frac{{{S_{CMO}}}}{{{S_{CMA}}}} = \frac{{{S_{BMO}}}}{{{S_{BMA}}}}\), vận dụng với các tam giác khác để được lời giải như trên.

Kẻ OR, AQ lần lượt là đường cao của tam giác CMO, CMA ứng với cạnh đáy CM.
Khi đó \({S_{CMO}} = \frac{1}{2}OR.CM\), \({S_{CMA}} = \frac{1}{2}AQ.CM\). Suy ra \(\frac{{{S_{CMO}}}}{{{S_{CMA}}}} = \frac{{\frac{1}{2}OR.CM}}{{\frac{1}{2}AQ.CM}} = \frac{{OR}}{{AQ}}\) (1)
Mặt khác, xét tam giác MAQ có OR // AQ, suy ra \(\frac{{OR}}{{AQ}} = \frac{{MO}}{{MA}}\) (hệ quả định lí Thales) (2)
Ta có \({S_{BMO}} = \frac{1}{2}OR.BM\), \({S_{BMA}} = \frac{1}{2}AQ.BM\). Suy ra \(\frac{{{S_{BMO}}}}{{{S_{BMA}}}} = \frac{{\frac{1}{2}OR.BM}}{{\frac{1}{2}AQ.BM}} = \frac{{OR}}{{AQ}}\) (3)
Từ (1), (2) và (3) suy ra \(\frac{{MO}}{{MA}} = \frac{{{S_{CMO}}}}{{{S_{CMA}}}} = \frac{{{S_{BMO}}}}{{{S_{BMA}}}}\).
Từ bài toán phụ trên, ta làm tương tự với các tam giác khác trong hình để được kết quả như lời giải.
Đáp án : D








Danh sách bình luận