Cho tam giác có là trung điểm của và là tia phân giác của góc . Khi đó, tam giác là tam giác gì?
-
A.
cân tại
-
B.
cân tại
-
C.
đều.
-
D.
cân tại
Ta sử dụng tính chất: Nếu một tam giác có đường trung tuyến trùng với đường phân giác thì tam giác đó là tam giác cân.
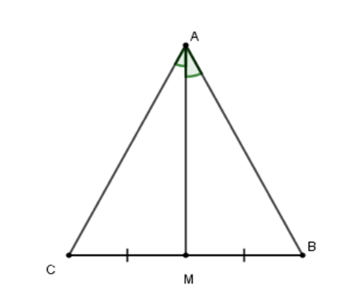
Tam giác có vừa là đường trung tuyến vừa là đường phân giác nên cân tại
Đáp án : D

Các bài tập cùng chuyên đề
Cho tam giác và tam giác có . Cần thêm một điều kiện gì để tam giác và tam giác bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông ?
Cho tam giác và tam giác có . Cần thêm một điều kiện gì để tam giác và tam giác bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề:
Cho tam gác và tam giác có . Phát biểu nào trong các phát biểu sau đây là đúng
Cho tam giác và tam giác có: . Phát biểu nào trong các phát biểu sau là đúng:
Cho tam giác và tam giác có , , . Biết Độ dài là:
Cho tam giác và tam giác có , , Biết . Số đo góc là:
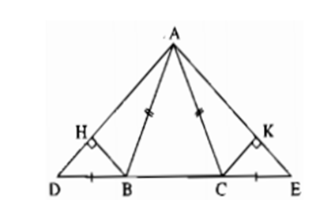
Cho hình vẽ sau. Chọn câu đúng.
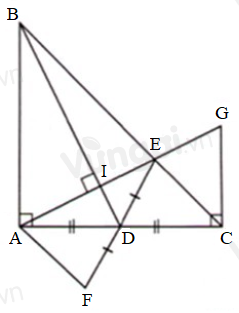
Cho tam giác vuông cân tại . Một đường thẳng bất kì luôn đi qua . Kẻ và vuông góc với đường thẳng Khi đó tổng bằng
Cho tam giác vuông cân tại và là trung điểm Từ kẻ đường vuông góc với cắt tại Chọn đáp án đúng.