Cho hai đoạn thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) là trung điểm của mỗi đoạn thẳng đó. Lấy \(E;\,F\) lần lượt là điểm thuộc đoạn \(AD\) và \(BC\) sao cho \(AE = BF.\) Cho \(OE = 2cm\), tính \(EF.\)
-
A.
\(4\,cm\)
-
B.
\(2cm\)
-
C.
$3\,cm$
-
D.
\(3,5\,cm\)
Dùng trường hợp bằng nhau thứ hai để chứng minh hai tam giác bằng nhau, từ đó có các cạnh và các góc tương ứng. Lập luận để có được \(O\) là trung điểm của \(EF\) để tính độ dài \(EF.\)
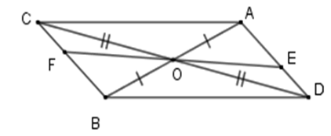
* Xét tam giác \(OBC\) và \(OAD\) có
+ \(OA = OB\,\left( {gt} \right)\)
+ \(\widehat {AOD} = \widehat {BOC}\) (đối đỉnh)
+ \(OC = OD\left( {gt} \right)\)
Suy ra \(\Delta OAD = \Delta OBC\left( {c - g - c} \right)\) nên \(\widehat {OAD} = \widehat {OBC}\) (hai góc tương ứng)
* Xét tam giác \(OBF\) và \(OAE\) có
+ \(OA = OB\,\left( {gt} \right)\)
+ \(\widehat {OAD} = \widehat {OBC}\) (cmt)
+ \(BF = AE\left( {gt} \right)\)
Suy ra \(\Delta OBF = \Delta OAE\left( {c - g - c} \right)\) nên \(OE = OF\) (hai cạnh tương ứng) và \(\widehat {AOE} = \widehat {FOB}\) (hai góc tương ứng)
Mà \(\widehat {FOB} + \widehat {FOA} = 180^\circ \) (hai góc kề bù) nên \(\widehat {FOA} + \widehat {AOE} = 180^\circ \)
Suy ra ba điểm \(F;\,O;E\) thẳng hàng và \(OE = OF\) nên \(O\) là trung điểm của \(EF \Rightarrow EF = 2.OE = 4\,cm.\)
Đáp án : A
Các bài tập cùng chuyên đề
Cho tam giác $ABC$ và tam giác $MHK$ có: $AB = MH$ , \(\widehat A = \widehat M\). Cần thêm một điều kiện gì để hai tam giác $ABC$ và $MHK$ bằng nhau theo trường hợp cạnh – góc – cạnh:
Cho tam giác $BAC$ và tam giác $KEF$ có $BA = EK,$ \(\widehat A = \widehat K\), $CA = KF.$ Phát biểu nào trong trong các phát biểu sau đây là đúng:
Cho hai đoạn thẳng $BD$ và $EC$ vuông góc với nhau tại $A$ sao cho $AB = AE,AD = AC,AB < AC.$ Phát biểu nào trong các phát biểu sau đây là sai:
Cho tam giác $DEF$ và tam giác $HKG$ có $DE = HK$ , \(\widehat E = \widehat K\), $EF = KG.$ Biết \(\widehat D = {70^0}\). Số đo góc $H$ là:
Cho tam giác $ABC$ có \(\widehat A = {90^0}\), tia phân giác $BD$ của góc $B$ (\(D \in AC\)). Trên cạnh $BC$ lấy điểm $E$ sao cho $BE = BA.$ Hai góc nào sau đây bằng nhau?
Cho đoạn thẳng \(AB\), trên đường trung trực \(d\) của đoạn \(AB\) lấy điểm \(M.\) So sánh \(AM\) và \(BM.\)
Cho tam giác $ABC$ có $M,N$ lần lượt là trung điểm của $AB,AC.$ Trên tia đối của tia $MC$ lấy $D$ sao cho $MD = MC$ . Trên tia đối của tia $NB$ lấy điểm $E$ sao cho $NE = NB.$
(I) \(\Delta AMD = \Delta BMC\)
(II) \(\Delta ANE = \Delta CNB\)
(III) $A,D,E$ thẳng hàng
(IV) $A$ là trung điểm của đoạn thẳng $DE$
Số khẳng định đúng trong các khẳng định trên là
Cho tam giác \(ABC\) có \(\widehat A = {90^0},M\) là trung điểm \(AC.\) Trên tia đối của tia \(MB\) lấy \(K\) sao cho \(MK = MB.\) Chọn câu đúng nhất:
