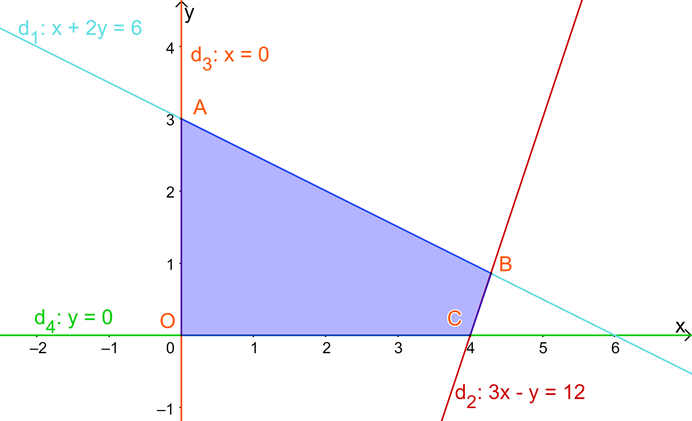
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y \le 6\\3x - y \le 12\\x \ge 0\\y \ge 0\end{array} \right.\) có miền nghiệm là miền tứ giác OABC như hình dưới. Giá trị lớn nhất của \(F = 28x + 49y\) là:
-
A.
\(0\)
-
B.
\(112\)
-
C.
\(147\)
-
D.
\(162\)
Bước 1: Xác định tọa độ các điểm O, A, B, C
Bước 2: Thay tọa độ các đỉnh vào biểu thức F, kết luận GTLN.
Ta có:
+) O là gốc tọa độ \( \Rightarrow O(0;0)\)
+) A là giao điểm của \({d_1}:x + 2y = 6\) và Oy \( \Rightarrow A(0;3)\)
+) B là giao điểm của \({d_1}:x + 2y = 6\) và \({d_2}:3x - y = 12\) \( \Rightarrow B(\frac{{30}}{7};\frac{6}{7})\)
+) C là giao điểm của \({d_2}:3x - y = 12\) và Ox \( \Rightarrow C(4;0)\)
Tại O: \(F = 28.0 + 49.0 = 0\)
Tại A (0; 3): \(F = 28.0 + 49.3 = 147\)
Tại \(B(\frac{{30}}{7};\frac{6}{7})\): \(F = 28.\frac{{30}}{7} + 49.\frac{6}{7} = 162\)
Tại C (4; 0): \(F = 28.4 + 49.0 = 112\)
Vậy giá trị lớn nhất của \(F=162\).
Đáp án : D
Các bài tập cùng chuyên đề
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
Cặp số nào sau đây là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}3x - 5y > 12\\x - 2y \le 7\end{array} \right.\)
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + 2(y + 1) - 4y \le 2(x + 1) - 5y\\x + y \ge 0\end{array} \right.\) không chứa điểm có tọa độ:
Điểm \(A(1;2)\) thuộc miền nghiệm của hệ bất phương trình nào sau đây?
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\2x + 3y > 6\end{array} \right.\) là phần không gạch trong hình nào dưới đây?
Phần tô màu trong hình dưới đây biểu diễn miền nghiệm của hệ bất phương trình nào?
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x + y \le 6\\3x - 4y \le 6\\5x - 2y \ge 0\\x \le 2\\y \ge - 1\end{array} \right.\)
có miền nghiệm là miền ngũ giác ABCDE như hình dưới. Giá trị nhỏ nhất của \(F = 15x - 9y\) là:
