Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
 Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Giải bài 4 trang 44 SGK Giải tích 12
Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:
Video hướng dẫn giải
Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:
LG a
\({x^3}-3{x^2} + 5 = 0\);
Phương pháp giải:
+) Khảo sát sự biến thiên của các hàm số \(y=f\left( x \right)\) lập bảng biến thiên, vẽ đồ thị hàm số.
+) Số nghiệm của phương trình \(f\left( x \right)=a\) là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) với đường thẳng \(y=a.\)
+) Khi đó dựa vào đồ thị hàm số để xác định số giao điểm và kết luận.
Lời giải chi tiết:
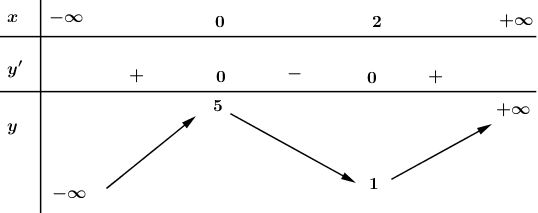
Xét hàm số: \(y={{x}^{3}}-3{{x}^{2}}+5\)
+) Tập xác định: \(D=R.\)
+) Sự biến thiên:
Ta có: \(y'=3{{x}^{2}}-6x\Rightarrow y'=0\) \(\Leftrightarrow 3{{x}^{2}}-6x=0\) \(\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=2 \\ \end{align} \right..\)
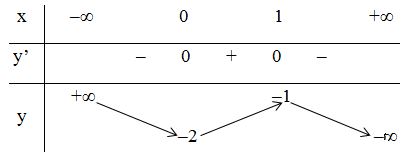
Hàm số đồng biến trên khoảng \(\left(- \infty ;0 \right)\) và \(\left( 2;+\infty \right)\); hàm số nghịch biến trên khoảng \(\left( 0;\ 2 \right).\)
Hàm số đạt cực đại tại \(x=0;\ \ {{y}_{CD}}=5.\)
Hàm số đạt cực tiểu tại \(x=2;\ \ {{y}_{CT}}=1.\)
+) Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ,\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
Bảng biến thiên:
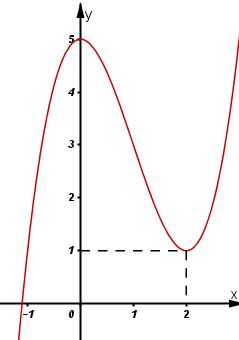
+) Đồ thị hàm số:
Đồ thị hàm số cắt trục \(Oy\) tại điểm \(\left( 0;\ 5 \right).\)
Số nghiệm của phương trình \({{x}^{3}}-3{{x}^{2}}+5=0\) là số giao điểm của đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}+5\) và trục hoành.
Từ đồ thị hàm số ta thấy đồ thị hàm số giao với trục hoành tại 1 điểm duy nhất.
Vậy phương trình đã cho có nghiệm duy nhất.
LG b
\(- 2{x^3} + 3{x^2}-2 = 0\) ;
Phương pháp giải:
Xét phương trình tương đương, sau đó:
+) Khảo sát sự biến thiên của các hàm số \(y=f\left( x \right)\) lập bảng biến thiên, vẽ đồ thị hàm số.
+) Số nghiệm của phương trình \(f\left( x \right)=a\) là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) với đường thẳng \(y=a.\)
+) Khi đó dựa vào đồ thị hàm số để xác định số giao điểm và kết luận.
Lời giải chi tiết:
\(-2{{x}^{3}}+3{{x}^{2}}-2=0.(*)\)
Ta có: (*) \(\Leftrightarrow 2{{x}^{3}}-3{{x}^{2}}=-2.\)
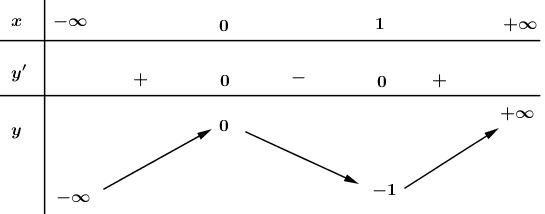
Xét hàm số: \(y=2{{x}^{3}}-3{{x}^{2}}.\)
Tập xác định: \(D=R.\)
Ta có: \(y'=6{{x}^{2}}-6x\) \(\Rightarrow y'=0\Leftrightarrow 6{{x}^{2}}-6x=0\) \(\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=1 \\ \end{align} \right..\)
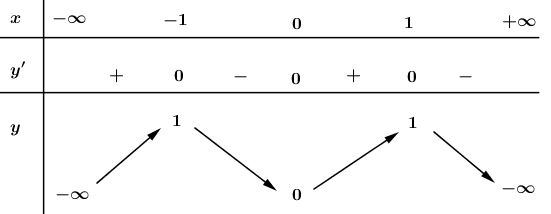
Hàm số đồng biến trên khoảng \(\left( -\infty ;\ 0 \right)\) và \(\left( 1;+\infty \right);\) nghịch biến trên khoảng \(\left( 0;\ 1 \right).\)
Hàm số đạt cực đại tại \(x=0;\ \ {{y}_{CD}}=0.\)
Hàm số đạt cực tiểu tại \(x=1;\ {{y}_{CT}}=-1.\)
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ,\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
Bảng biến thiên:
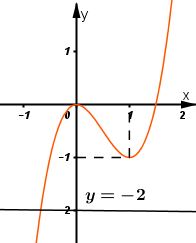
Đồ thị:
Số nghiệm của phương trình \(-2{{x}^{3}}+3{{x}^{2}}-2=0\) là số giao điểm của đồ thị hàm số \(y=2{{x}^{3}}-3{{x}^{2}}\) và đường thẳng \(y=-2.\)
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y=-2\) cắt đồ thị hàm số \(y=2{{x}^{3}}-3{{x}^{2}}\) tại 1 điểm duy nhất.
Vậy phương trình đã cho có nghiệm duy nhất.
Cách khác:
Xét hàm số \(y = {\rm{ }}f\left( x \right) = - 2{x^3}\; + {\rm{ }}3{x^2}-2.\)
- TXĐ: \(D = \mathbb R\)
- Sự biến thiên:
+ Chiều biến thiên:
\(\begin{array}{*{20}{l}}
{y' = - 6{x^2}\; + {\rm{ }}6x = - 6x\left( {x - 1} \right)}\\
{y' = 0{\rm{ }} \Leftrightarrow {\rm{ }}x = 0{\rm{ }};{\rm{ }}x = 1}
\end{array}\)
+ Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty ,\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \)
+ Bảng biến thiên:
- Đồ thị:
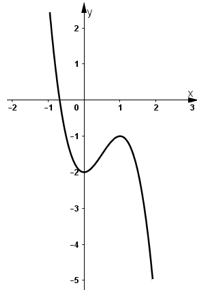
Đồ thị hàm số \(y = f(x)\) cắt trục hoành tại 1 điểm duy nhất
⇒ phương trình \(f(x) = 0)\) có nghiệm duy nhất.
Vậy phương trình \( - 2{x^3}\; + 3{x^2}\; -2 = 0\) chỉ có một nghiệm.
LG c
\(2{x^2}-{x^4} = - 1\).
Phương pháp giải:
+) Khảo sát sự biến thiên của các hàm số \(y=f\left( x \right)\) lập bảng biến thiên, vẽ đồ thị hàm số.
+) Số nghiệm của phương trình \(f\left( x \right)=a\) là số giao điểm của đồ thị hàm số \(y=f\left( x \right)\) với đường thẳng \(y=a.\)
+) Khi đó dựa vào đồ thị hàm số để xác định số giao điểm và kết luận.
Lời giải chi tiết:
\(2{{x}^{2}}-{{x}^{4}}=-1.\)
Xét hàm số: \(y=2{{x}^{2}}-{{x}^{4}}.\)
Tập xác định: \(D=R.\)
Sự biến thiên: \(y'=4x-4{{x}^{3}}\Rightarrow y'=0\) \(\Leftrightarrow 4x-4{{x}^{3}}=0\Leftrightarrow \left[ \begin{align}& x=0 \\ & x=\pm 1 \\ \end{align} \right..\)
Hàm số đồng biến trên khoảng \(\left( -\infty ;\ -1 \right)\) và \(\left( 0;\ 1 \right);\) hàm số nghịch biến trên khoảng \(\left( -1;\ 0 \right)\) và \(\left( 1;+\infty \right).\)
Hàm số đạt cực đại tại hai điểm \(x=-1\) và \(x=1;\ \ {{y}_{CD}}=1.\)
Hàm số đạt cực tiểu tại \(x=0;\ {{y}_{CT}}=0.\)
Giới hạn:\(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ,\mathop {\lim }\limits_{x \to + \infty } y = - \infty \)
Bảng biến thiên:
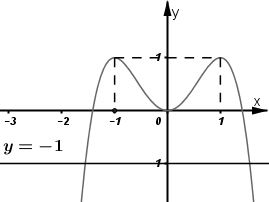
Đồ thị:
Số nghiệm của phương trình \(2{{x}^{2}}-{{x}^{4}}=-1\) là số giao điểm của đồ thị hàm số \(y=2{{x}^{2}}-{{x}^{4}}\) và đường thẳng \(y=-1.\)
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y=-1\) cắt đồ thị hàm số \(y=2{{x}^{2}}-{{x}^{4}}\) tại hai điểm phân biệt.
Vậy phương trình đã cho có 2 nghiệm phân biệt.
Loigiaihay.com
- Giải bài 5 trang 44 SGK Giải tích 12
- Giải bài 6 trang 44 SGK Giải tích 12
- Giải bài 7 trang 44 SGK Giải tích 12
- Giải bài 8 trang 44 SGK Giải tích 12
- Giải bài 9 trang 44 SGK Giải tích 12
>> Xem thêm