-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Giải bài 9 trang 44 SGK Giải tích 12
Cho hàm số
Video hướng dẫn giải
Cho hàm số \(y=\frac{(m+1)x-2m+1}{x-1}\) (m là tham số) có đồ thị là \((G)\).
LG a
a) Xác định \(m\) để đồ thị \((G)\) đi qua điểm \((0 ; -1)\).
Phương pháp giải:
\(y = f(x)\).Thay \(x= 0, y =-1\) vào biểu thức trên để tìm m
Lời giải chi tiết:
Theo đề bài ta có \((0 ; -1) ∈ (G) \) \(⇔ -1=\dfrac{(m+1)\cdot 0-2m+1}{0-1}\) \( \Leftrightarrow - 1 = 2m - 1 \Leftrightarrow 2m = 0\) \(\Leftrightarrow m=0.\)
Quảng cáo
LG b
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với \(m\) tìm được.
Phương pháp giải:
Thay giá trị m đã tìm được ở câu a vào đồ thị hàm số sau đó khảo sát và vẽ đồ thị hàm số.
Lời giải chi tiết:
Với \(m = 0\) ta được hàm số \(y=\dfrac{x+1}{x-1}\) (G0).
Tập xác định: \(D=\mathbb R \backslash {\rm{\{ }}1\}\)
* Sự biến thiên:
Ta có: \(y' = {{ - 2} \over {{{(x - 1)}^2}}} < 0\forall x \in D\)
- Hàm số nghịch biến trên khoảng: \((-\infty;1)\) và \((1;+\infty)\).
- Cực trị:
Hàm số không có cực trị.
- Tiệm cận:
\(\eqalign{
& \mathop {\lim y}\limits_{x \to \pm \infty } = 1 \cr
& \mathop {\lim y}\limits_{x \to {1^ - }} = - \infty \cr
& \mathop {\lim y}\limits_{x \to {1^ + }} = + \infty \cr} \)
Tiệm cận đứng là: \(x=1\), tiệm cận ngang là: \(y=1\)
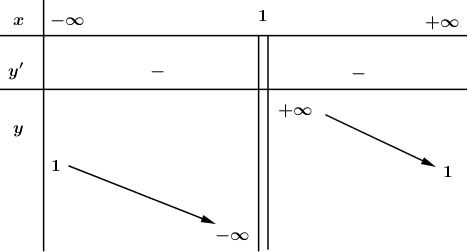
- Bảng biến thiên:
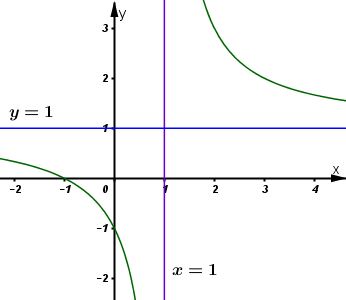
* Đồ thị:
Đồ thị hàm số giao trục \(Ox\) tại \((-1;0)\), trục \(Oy\) tại \((0;-1)\)
Đồ thị hàm số nhận \(I(1;1)\) làm tâm đối xứng.
LG c
c) Viết phương trình tiếp tuyến của đồ thị trên tại giao điểm của nó với trục tung.
Phương pháp giải:
Đồ thị hàm số cắt trục tung tại điểm có M tung độ \(y = y_0 \Rightarrow M(0;y_0) \).
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại \(M\left( {{x_0};{y_0}} \right)\) bằng công thức: \(y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\).
Lời giải chi tiết:
(G0) cắt trục tung tại \(M(0 ; -1)\).
\(y'=\dfrac{-2}{(x-1)^{2}}\Rightarrow y'(0) = -2\).
Phương trình tiếp tuyến của (G0) tại \(M\) là: \(y - (-1) = y'(0)(x - 0) \) \(⇔ y= -2x - 1\)
Loigiaihay.com
Bình luận
Chia sẻ
- Khảo sát và vẽ đồ thị hàm số bậc ba
- Khảo sát và vẽ đồ thị hàm bậc bốn trùng phương
- Khảo sát và vẽ đồ thị hàm phân thức hữu tỉ
- Các dạng toán về khảo sát hàm số bậc ba, bậc bốn trùng phương
- Giải bài 8 trang 44 SGK Giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
