Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ..

Bài 38 trang 82 SGK Toán 9 tập 2


Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB

Đề bài

Trên một đường tròn, lấy liên tiếp ba cung \(AC, CD, DB\) sao cho

\(sđ\overparen{AC}=sđ\overparen{CD}=sđ\overparen{DB}=60^0\). Hai đường thẳng \(AC\) và \(BD\) cắt nhau tại \(E\). Hai tiếp tuyến của đường tròn tại \(B\) và \(C\) cắt nhau tại \(T\). Chứng minh rằng:

a) \(\widehat {AEB}=\widehat {BTC}\);

b) \(CD\) là phân giác của \(\widehat{BCT}.\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.

+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

+) Số đo góc nội tếp bằng nửa số đo cung bị chắn

Lời giải chi tiết

 

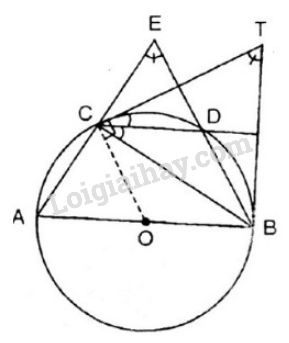
a) Xét đường tròn \((O)\) có \(sđ\overparen{AC}=sđ\overparen{CD}=sđ\overparen{DB}=60^0\) nên \(sđ\overparen{AB}=sđ\overparen{AC}+sđ\overparen{CD}+sđ\overparen{DB}\)\(=60^0+60^0+60^0=180^0.\)

Ta có \(\widehat{AEB}\) là góc có đỉnh ở bên ngoài đường tròn chắn cung \(CD\) và \(AB\) nên:

\(\displaystyle \widehat{AEB}=\dfrac{sđ\overparen{AB}- sđ\overparen{CD}}{2}={{{{180}^0 - {{60}^0}}} \over 2} = {60^0}.\)  

và \(\widehat{BTC}\)  cũng là góc có đỉnh ở bên ngoài đường tròn chắn cung \(BC\) lớn và \(BC\) nhỏ (hai cạnh đều là tiếp tuyến của đường tròn) nên:

\(\widehat{BTC}=\dfrac{sđ\overparen {BAC}-sđ\overparen{BDC}}{2}\)\(\displaystyle = {{({{180}^0} + {{60}^0}) - ({{60}^0} + {{60}^0})} \over 2} = {60^0}.\)  

 Vậy \(\widehat {AEB} =\widehat {BTC}=60^0.\) 

b) Xét đường tròn \((O)\) có:

\(\widehat {DCT} \) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(CD\) nên:

 \(\widehat {DCT}=\dfrac{sđ\overparen{CD}}{2}=\dfrac{60^0}{2}=30^0.\)

\(\widehat {DCB}\) là góc nội tiếp chắn cung \(BD\) nên: \(\displaystyle \widehat {DCB}=\dfrac{sđ\overparen{DB}}{2}={{{{60}^0}} \over 2} = {30^0}.\)

Vậy  \(\widehat {DCT}=\widehat {DCB}=30^0\) \(= \dfrac{1}{2}\). \(\widehat {BCT}\)hay  \(CD\) là phân giác của \(\widehat {BCT}. \)


Bình chọn:
4.4 trên 173 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store