Bài 22 trang 76 SGK Toán 9 tập 2
Trên đường tròn (O) đường kính AB
Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD
Đề bài
Trên đường tròn \((O)\) đường kính \(AB\), lấy điểm \(M\) (khác \(A\) và \(B\)). Vẽ tiếp tuyến của (O) tại \(A\). Đường thẳng \(BM\) cắt tiếp tuyến đó tại \(C\). Chứng minh rằng ta luôn có: \(M{A^2} = MB.MC\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Sử dụng hệ thức lượng trong tam giác vuông
+ Hoặc ta chứng minh \(\Delta {\rm M}{\rm A}{\rm B}\) đồng dạng với \(\Delta MCA\) từ đó suy ra tỉ lệ cạnh để có đẳng thức cần chứng minh.
Lời giải chi tiết
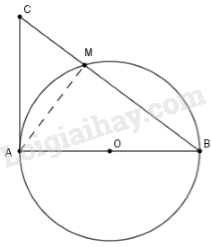
Xét \(\left( O \right)\) có \(\widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) suy ra \(AM \bot BC\)
Lại có \(AC\) là tiếp tuyến tại A nên \(\widehat {BAC} = 90^\circ \)
Xét tam giác ABC vuông tại A có AM là đường cao, theo hệ thức lượng trong tam giác vuông ta có:
\(M{A^2} = MB.MC\) (đpcm)
Cách khác:
+ Xét \(\left( O \right)\) có \(\widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) suy ra \(AM \bot BC \Rightarrow \widehat {CMA} = 90^\circ \).
Lại có \(AC\) là tiếp tuyến nên \(\widehat {BAC} = 90^\circ .\)
+ Ta có \(\widehat {MBA} + \widehat {MAB} = 90^\circ \) (vì tam giác \(MAB\) vuông tại \(M\) ) và \(\widehat {MAB} + \widehat {MAC} = 90^\circ \) (do \(\widehat {BAC} = 90^\circ \)) nên \(\widehat {MBA} = \widehat {MAC}\)
+ Xét \(\Delta MAB\) và \(\Delta MCA\) có \(\widehat M\) chung và \(\widehat {MBA} = \widehat {MAC}\) (cmt) nên \(\Delta {\rm M}{\rm A}{\rm B}\) đồng dạng với \(\Delta MCA\left( {g - g} \right)\) suy ra \(\dfrac{{MA}}{{MC}} = \dfrac{{MB}}{{MA}} \Rightarrow M{A^2} = MB.MC\) (đpcm)
Loigiaihay.com
- Bài 23 trang 76 SGK Toán 9 tập 2
- Bài 24 trang 76 SGK Toán 9 tập 2
- Bài 25 trang 76 SGK Toán 9 tập 2
- Bài 26 trang 76 SGK Toán 9 tập 2
- Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 3 - Hình học 9
>> Xem thêm
Các bài khác cùng chuyên mục




















