Một học sinh tiến hành một thí nghiệm, trong đó, bạn ấy treo một quả bóng khối lượng m bằng một sợi dây và quay đều nó chuyển động theo một đường tròn. Qủa bóng được đẩy ra khỏi tâm của vòng tròn chuyển động bằng một lực li tâm FT. Lực được mô tả bằng công thức \({F_T} = \frac{{m{v^2}}}{R}\), với m là khối lượng, v là tốc độ của quả bóng và R là bán kính chuyển động của nó.
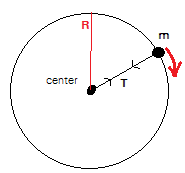
Một học sinh tiến hành một thí nghiệm, trong đó, bạn ấy treo một quả bóng khối lượng m bằng một sợi dây và quay đều nó chuyển động theo một đường tròn. Qủa bóng được đẩy ra khỏi tâm của vòng tròn chuyển động bằng một lực li tâm FT. Lực được mô tả bằng công thức \({F_T} = \frac{{m{v^2}}}{R}\), với m là khối lượng, v là tốc độ của quả bóng và R là bán kính chuyển động của nó.

Một điểm A nằm trên vành tròn chuyển động với vận tốc 50cm/s, điểm B nằm cùng trên bán kính với điểm A chuyển động với vận tốc 10cm/s. Biết AB = 20 cm. Tính gia tốc hướng tâm của hai điểm A, B:
Một điểm A nằm trên vành tròn chuyển động với vận tốc 50cm/s, điểm B nằm cùng trên bán kính với điểm A chuyển động với vận tốc 10cm/s. Biết AB = 20 cm. Tính gia tốc hướng tâm của hai điểm A, B:
\({a_A} = 20cm/{s^2};{a_B} = 100cm/{s^2}\)
\({a_A} = 150cm/{s^2};{a_B} = 30cm/{s^2}\)
\({a_A} = 100cm/{s^2};{a_B} = 20cm/{s^2}\)
\({a_A} = 30cm/{s^2};{a_B} = 150cm/{s^2}\)
Đáp án: C
vA = 50cm/s; vB = 10cm/s; AB = 20cm.
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{v_A} = {R_A}.\omega }\\{{v_B} = {R_B}.\omega }\\{{R_A} - {R_B} = AB}\end{array}} \right. \Rightarrow {v_A} - {v_B} = \left( {{R_A} - {R_B}} \right)\omega {\rm{\;}} \Rightarrow \omega {\rm{\;}} = \frac{{{v_A} - {v_B}}}{{{R_A} - {R_B}}} = \frac{{50 - 10}}{{20}} = 2rad/s\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{R_A} = \frac{{{v_A}}}{\omega } = \frac{{50}}{2} = 25cm}\\{{R_B} = \frac{{{v_B}}}{\omega } = \frac{{10}}{2} = 5cm}\end{array}} \right.\)
→ Gia tốc hướng tâm: \(\left\{ {\begin{array}{*{20}{l}}{{a_A} = {R_A}{\omega ^2} = 100cm/{s^2}}\\{{a_B} = {R_B}{\omega ^2} = 20cm/{s^2}}\end{array}} \right.\)

- Tại một thời điểm trong thí nghiệm của học sinh, m bằng một giá trị nhất định x; v bằng một giá trị nhất định y và R bằng một giá trị nhất định z. Lực kết quả tính được là 20 N (đơn vị của lực). Chúng ta có thể dự đoán lực là bao nhiêu nếu học sinh chọn giảm một nửa vận tốc, tăng gấp đôi khối lượng và giữa nguyên giá trị của bán kính?
- Tại một thời điểm trong thí nghiệm của học sinh, m bằng một giá trị nhất định x; v bằng một giá trị nhất định y và R bằng một giá trị nhất định z. Lực kết quả tính được là 20 N (đơn vị của lực). Chúng ta có thể dự đoán lực là bao nhiêu nếu học sinh chọn giảm một nửa vận tốc, tăng gấp đôi khối lượng và giữa nguyên giá trị của bán kính?
20N
5N
10N
40N
Đáp án: C
- Trước tiên, chúng ta bỏ qua các biến vì chúng là thông tin không cần thiết.
Ta có: \({F_T} = \frac{{m{v^2}}}{R}\)
Giảm một nửa vận tốc => \(v' = \frac{v}{2}\)
Tăng gấp đôi khối lượng => m’ = 2m
Bán kính R giữ nguyên
Suy ra: \(F{'_T} = \frac{{2m{{\left( {\frac{v}{2}} \right)}^2}}}{R} = \frac{1}{2}.\frac{{m{v^2}}}{R} = \frac{{{F_T}}}{2} = \frac{{20}}{2} = 10N\)
Mối quan hệ giữa lực trong sợi dây và khối lượng của quả cầu là gì?
Mối quan hệ giữa lực trong sợi dây và khối lượng của quả cầu là gì?
Mối quan hệ tuyến tính tích cực
Mối quan hệ tuyến tính phủ định
Mối quan hệ tiêu cực, theo cấp số nhân
Không có mối quan hệ rõ ràng
Đáp án: A
Câu trả lời đúng là nó là một mối quan hệ tích cực, tuyến tính.
Như chúng ta có thể thấy trong phương trình, F tỉ lệ thuận với m không có số mũ liên quan. Điều này có nghĩa là nếu chúng ta tăng gấp đôi khối lượng thì lực cũng tăng lên gấp đôi.
Biết rằng sợi dây có chiều dài 1m, quả bóng được quay đều với tốc độ 60 vòng/phút. Thời gian để quả bóng quay hết một vòng là:
Biết rằng sợi dây có chiều dài 1m, quả bóng được quay đều với tốc độ 60 vòng/phút. Thời gian để quả bóng quay hết một vòng là:
2s
1s
3,14s
6,28s
Đáp án: B
Từ đầu bài ta có: Tốc độ góc \(\omega {\rm{\;}} = 60\) vòng/phút \( = 60.\frac{{2\pi }}{{60}} = 2\pi \left( {ra{\rm{d}}/s} \right)\)
Mặt khác: \(\omega {\rm{\;}} = \frac{{2\pi }}{T}\)
Suy ra, thời gian quả bóng quay hết một vòng là:
\(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1{\rm{s}}\)
Chuyển động tròn là
Chuyển động tròn là
Chuyển động có quỹ đạo là một đường tròn
Chuyển động có hướng không đổi
Chuyển động có chiều chuyển động luôn không đổi
Chuyển động có gia tốc bằng 0
Đáp án: A
Vận dụng lý thuyết về chuyển động tròn đều
Chuyển động tròn là chuyển động có quỹ đạo là một đường tròn
Công thức nào sau đây biểu diễn không đúng quan hệ giữa các đại lượng đặc trưng của một vật chuyển động tròn đều?
Công thức nào sau đây biểu diễn không đúng quan hệ giữa các đại lượng đặc trưng của một vật chuyển động tròn đều?
\(f = \frac{{2\pi r}}{v}\)
\(T = \frac{{2\pi r}}{v}\)
\(v = \omega r\)
\(\omega {\rm{\;}} = \frac{{2\pi }}{T}\)
Đáp án: A
Ta có:
+ Vận tốc dài và tốc độ góc:
\(v = \omega r\)
+ Tốc độ góc: \(\omega {\rm{\;}} = \frac{{2\pi }}{T}\)
+ Chu kì và tần số: \(f = \frac{1}{T}\)
Từ đây, ta suy ra các phương án:
B, C, D - đúng
A - sai vì: \(f = \frac{1}{T} = \frac{\omega }{{2\pi }} = \frac{v}{{2\pi r}}\)







