Một cái sân hình vuông ABCD có cạnh là 8 m. Người ta muốn lát gạch màu khác để trang trí lên mảnh sân hình vuông MNPQ nội tiếp trong sân hình vuông ABCD. Tìm vị trí của M, N, P, Q để hình vuông MNPQ có diện tích nhỏ nhất.
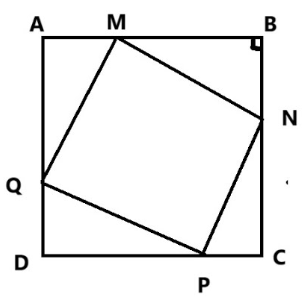
Diện tích hình vuông MNPQ nhỏ nhất khi tổng diện tích S của 4 tam giác vuông ở 4 góc hình vuông ABCD lớn nhất.
Lập công thức tính diện tích tổng 4 tam giác, áp dụng bất đẳng thức Cauchy để tìm giá trị lớn nhất.
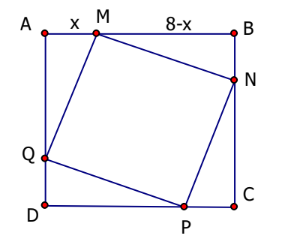
Đặt AM = x (0 < x < 8, đơn vị: mét), khi đó MB = 8 – x (m).
Ta có \(\Delta AMQ = \Delta BNM = \Delta CPN = \Delta DQP\).
Diện tích hình vuông MNPQ nhỏ nhất khi tổng diện tích S của 4 tam giác vuông ở 4 góc hình vuông ABCD lớn nhất.
Ta có \(S = 4.\frac{1}{2}AM.AQ = 2AM.AQ = 2AM.MB\) \(\left( {{m^2}} \right)\).
Áp dụng bất đẳng thức Cauchy cho hai số dương là độ dài đoạn thẳng AM và MB, ta có:
\(A{M^2} + M{B^2} \ge 2AM.MB\)
\(A{M^2} + 2AM.MB + M{B^2} \ge 4AM.MB\)
\({\left( {AM + MB} \right)^2} \ge 4AM.MB\)
\(2AM.MB \le \frac{{{{\left( {AM + MB} \right)}^2}}}{2}\)
\(S \le \frac{{{8^2}}}{2}\)
\(S \le 32\).
Dấu “=” xảy ra khi \(AM = MB = \frac{{AB}}{2} = \frac{8}{2} = 4\).
Vậy, khi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA thì hình vuông MNPQ có diện tích nhỏ nhất.








Danh sách bình luận