Gieo một đồng xu cân đối liên tiếp bốn lần.
a) Vẽ sơ đồ hình cây mô tả không gian mẫu.
b) Tính xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa.
a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây:
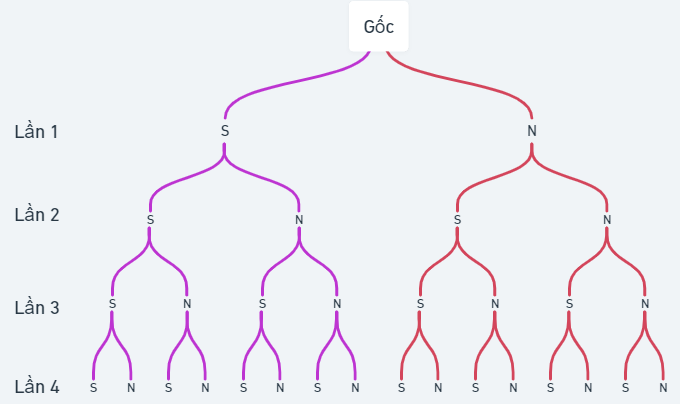
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”.
Suy ra \(A = \left\{ {SSNN;SNSN;SNNS;NSSN;NSNS;NNSS} \right\}\). Suy ra \(n\left( A \right) = 6\). Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).

Các bài tập cùng chuyên đề
Gieo liên tiếp một con xúc xắc và một đồng xu.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của các biến cố sau: F: “Đồng xu xuất hiện mặt ngửa"; G: “Đồng xu xuất hiện mặt sấp hoặc Số chấm xuất hiện trên con xúc xắc là 5".
Trên một phố có hai quán ăn X, Y. Ba bạn Sơn, Hải, Văn mỗi người chọn ngẫu nhiên một quán ăn.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của biến cố “Hai bạn vào quán X, bạn còn lại vào quán Y".
Dự báo thời tiết trong ba ngày thứ Hai, thứ Ba, thứ Tư của tuần sau cho biết, trong mỗi ngày này, khả năng có mưa và không mưa như nhau.
a) Vẽ sơ đồ hình cây mô tả không gian mẫu.
b) Tính xác suất của các biến cố:
F: “Trong ba ngày, có đúng một ngày có mưa”
G: “Trong ba ngày, có ít nhất hai ngày không mưa”.
Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh, 1 thẻ đỏ. Các tấm thẻ có kích thước có khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.
a) Sử dụng sơ đồ hình cây, hãy liệt kê tất cả các kết quả có thể xảy ra.
b) Tính xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”.
Chỉ có 1 cái ô xanh, 1 cái ô trắng, 1 cái mũ xanh, 1 cái mũ trắng, 1 cái mũ đen, 1 đôi giày đen, 1 đôi giày trắng. Chi chọn ngẫu nhiên 1 cái ô, 1 cái mũ và 1 đôi giày để đến trường.
a) Hãy vẽ sơ đồ mô tả các kết quả có thể xảy ra.
b) Tính xác suất của biến cố “Chỉ có 1 trong 3 thứ đồ Chi chọn có màu trắng”.
Trên một dãy phố có 3 quán ăn A, B, C. Hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán để ăn trưa.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của các biến cố sau:
E: “Hai người cùng vào một quán".
F: “Cả hai không chọn quán C.
Trên một phố có hai quán ăn A, B. Bốn bạn Sơn, Hải, Văn, Đạo mỗi người chọn ngẫu nhiên một quán ăn.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất để:
• Tất cả đều vào một quán;
• Mỗi quán có đúng 2 bạn vào;
• Quán A có 3 bạn vào, quán B có 1 bạn vào;
• Một quán có 3 bạn vào, quán kia có 1 bạn vào.







Danh sách bình luận