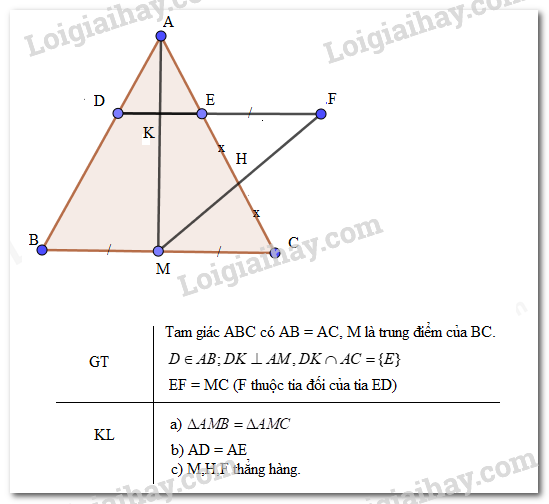
Cho tam giác ABC có AB = AC, M là trung điểm của BC.

a) Chứng minh rằng: \(\Delta AMB = \Delta AMC\)

b) Trên cạnh AB lấy điểm D. Từ D kẻ đường thẳng vuông góc với AM tại K và kéo dài cắt cạnh AC tại E. Chứng minh AD = AE.

c) Trên tia đối của tia ED lấy điểm F sao cho EF = MC, gọi H là trung điểm của EC. Chứng minh ba điểm M, H, F thẳng hàng.

 

a) Xét \(\Delta AMB\) và \(\Delta AMC\)có:

MB = MC (gt)

AM chung

AB = AC (gt)

\( \Rightarrow \Delta AMB = \Delta AMC(c.c.c)\)

b) Vì \(\Delta AMB = \Delta AMC(cmt) \Rightarrow \widehat {BAM} = \widehat {CAM}\) (2 góc tương ứng)

Xét \(\Delta ADK\) và \(\Delta AEK\)có:

\(\widehat {AKD} = \widehat {AKE}( = 90^\circ )\)

AK chung

\(\widehat {DAK} = \widehat {EAK}(cmt)\)

\( \Rightarrow \Delta ADK = \Delta AEK(g.c.g)\)

Do đó, AD = AE (2 cạnh tương ứng)

c) Vì \(\Delta AMB = \Delta AMC(cmt) \Rightarrow \widehat {BMA} = \widehat {CMA}\)(2 góc tương ứng)

Mà \(\widehat {BMA} + \widehat {CMA} = 180^\circ \) (2 góc kề bù)

\(\widehat {BMA} = \widehat {CMA} = 90^\circ  \Rightarrow AM \bot BC\)

Mà \(AM \bot DE(gt)\)

\( \Rightarrow DE//BC\).

\( \Rightarrow \widehat {HEF} = \widehat {HCM}\) (2 góc so le trong)

Xét \(\Delta HEF\) và \(\Delta HCM\)có:

EF = CM (gt)

\(\widehat {HEF} = \widehat {HCM}(cmt)\)

HE = HC (gt)

\( \Rightarrow \Delta HEF = \Delta HCM(c.g.c)\)

\( \Rightarrow \widehat {FHE} = \widehat {MHC}\) (2 góc tương ứng)

Mà \(\widehat {FHE} + \widehat {FHC} = 180^\circ \) (2 góc kề bù)

\( \Rightarrow \widehat {MHC} + \widehat {FHC} = 180^\circ \)

Do đó, M,H,F thẳng hàng.