Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.
a) Có bao nhiêu cách viết ngẫu nhiên một số tự nhiên như vậy?
b) Tính xác suất của mỗi biến cố “Số tự nhiên được viết ra là số tròn trăm”.
Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.
a) Có bao nhiêu cách viết ngẫu nhiên một số tự nhiên như vậy?
b) Tính xác suất của mỗi biến cố “Số tự nhiên được viết ra là số tròn trăm”.
a) Các số tự nhiên có hai chữ số nhỏ hơn 200 là: 10; 11; …; 199.
Áp dụng công thức tính số số hạng để tính:
Công thức tính số số hạng bằng (số cuối - số đầu) : khoảng cách + 1
b) Liệt kê các số tròn trăm
Để tính xác suất của biến cố “Số tự nhiên được viết ra là số tròn trăm”, ta lấy số lần xuất hiện số tròn trăm chia cho số số hạng của dãy số từ 10 đến 200.
a) Các số tự nhiên có hai chữ số nhỏ hơn 200 là: 10; 11; …; 199 .
Vậy có 190 cách viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 200.
b) Có 9 kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là số tròn trăm” là 100 ; 200 ; 300 ; 400 ; 500 ; 600 ; 700 ; 800 ; 900.
Do đó, xác suất của biến cố “Số tự nhiên được viết ra là số tròn trăm” là: \(\frac{9}{190}\) .

Các bài tập cùng chuyên đề
Một cửa hàng thống kê số lượng các loại điện thoại bán được trong một năm vừa qua như sau:
|
Loại điện thoại |
A |
B |
C |
|
Số lượng bán được (chiếc) |
712 |
1035 |
1085 |
Tính xác suất thực nghiệm của biến cố E: "Chiếc điện thoại loại A được bán ra trong năm đó của cửa hàng"
Ông An theo dõi và thống kê số cuộc gọi điện thoại đến cho ông trong 1 ngày. Sau 59 ngày theo dõi, kết quả thu được như sau:
|
Số cuộc điện thoại gọi đến trong một ngày |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Số ngày |
5 |
9 |
15 |
10 |
5 |
6 |
4 |
2 |
3 |
Gọi A là biến cố "Trong một ngày ông An nhận được nhiều hơn 6 cuộc gọi". Hỏi trong 59 ngày có bao nhiêu ngày biến cố A xuất hiện
Tung một chiếc kẹp giấy 145 lần xuống sàn nhà lát gạch đá hoa hình vuông. Quan sát thấy có 113 lần chiếc kẹp nằm hoàn toàn bên trong hình vuông và 32 lần chiếc kẹp nằm trên cạnh hình vuông. Tính xác suất thực nghiệm của các biến cố sau:
a) E: " Chiếc kẹp giấy nằm hoàn toàn trong hình vuông"
b) F: "Chiếc kẹp giấy nằm trên cạnh của hình vuông"
Một nhân viên kiểm tra chất lượng sản phẩm tại một nhà máy trong 20 ngày rồi ghi lại số phế phẩm của nhà máy và thu được kết quả như sau:
|
Số phế phẩm |
0 |
1 |
2 |
3 |
≥4 |
|
Số ngày |
14 |
3 |
1 |
1 |
1 |
Tính xác suất thực nghiệm của các biến cố sau:
a) M: "Trong một ngày nhà máy đó không có phế phẩm"
b) N: "Trong một ngày nhà máy đó chỉ có 1 phế phẩm"
c) K: "Trong một ngày nhà máy đó có ít nhất 2 phế phẩm"
Thống kê thời gian của 78 chương trình quảng cáo trên Đài truyền hình tỉnh X cho kết quả như sau:
|
Thời gian quảng cáo trong khoảng |
Số chương trình quảng cáo |
|
Từ 0 đến 19 giây |
17 |
|
Từ 20 đến 39 giây |
38 |
|
Từ 40 đến 59 giây |
19 |
|
Trên 60 giây |
4 |
Tính xác suất thực nghiệm của các biến cố sau:
a) E: "Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài từ 20 đến 39 giây"
b) F: "Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài trên 1 phút"
c) G:" Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài trong khoảng từ 20 đến 59 giây"
Trong trò chơi "Xúc xắc may mắn" ở mỗi ván chơi, người chơi gieo đồng thời hai con xúc xắc và ghi lại tổng số chấm xuất hiện trên hai con xúc xắn. Một người chơi 80 ván và ghi lại kết quả trong bảng sau:
|
Tổng số chấm |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Số ván |
2 |
5 |
6 |
8 |
11 |
14 |
12 |
9 |
6 |
4 |
3 |
a) Giả sử người chơi thắng nếu tổng số chấm xuất hiện trên hai con xúc xắc là 5 hoặc 7. Tính xác suất thực nghiệm của biến cố E: "Người chơi thắng trong một ván chơi"
b) Giả sử người chơi thắng nếu tổng số chấm xuất hiện trên hai con xúc xắc từ 10 trở lên. Tính xác suất thực nghiệm của biến cố F: "Người chơi thắng trong một ván chơi"
Một túi đựng các viên bi giống hệt nhau, chỉ khác màu, trong đó có 5 viên bi màu xanh, 3 viên bi màu đỏ và 7 viên bi màu trắng. Bạn Việt lấy ngẫu nhiên một viên bi trong túi. Tính xác suất của các biến cố sau
a) E: "Việt lấy được viên bi màu xanh"
b) F: "Việt lấy được viên bi màu đỏ"
c) G: "Việt lấy được viên bi màu trắng"
d) H: "Việt lấy được viên bi màu xanh hoặc màu đỏ"
e) K: "Việt không lấy được viên bi màu đỏ"
Trước khi Hà tung một đồng xu cân đối và đồng chất 100 lần, Thọ dự đoán sẽ có trên 70 lần xuất hiện mặt sấp còn Thúy lại dự đoán sẽ có ít hơn 70 lần xuất hiện mặt sấp. Theo em, bạn nào có khả năng dự đoán cao hơn? Vì sao?
Một hộp kín chứ 3 quả bóng xanh và 2 quả bóng đỏ có cùng kích thước và khối lượng An lấy ra ngẫu nhiên 1 quả bóng từ hộp, xem màu rồi trả lại hộp.
a) Tính tỉ số mô tả xác suất lí thuyết của biến cố “An lấy được bóng xanh”.
b) Sau khi lặp lại phép thử đó 100 lần, An ghi lại số lần mình lấy được bóng xanh sau 20; 40; 60; 80 và 100 lần lấy bóng như sau:

Tính các xác suất thực nghiệm của sự kiện “An lấy được bóng xanh” sau 20; 40; 60; 80 và 100 lần thử.
Phương gieo một con xúc xắc 120 lần và thống kê lại kết quả các lần gieo ở bảng sau:

Hãy tính xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm là số lẻ” sau 120 lần thử trên.
Một hộp chứa các thẻ màu xanh và thr màu đỏ có kích thước và khối lượng như nhau. Thọ lấy ra ngẫu nhiên 1 thẻ từ hộp, xem màu rồi trả lại hộp. Lặp lại thử nghiệm đó 50 lần. Thọ thấy có 14 lần lấy được thẻ màu xanh. Xác suất thực nghiệm của biến cố “Lấy được thẻ màu đỏ” là
A. 0,14.
B. 0,28.
C. 0,72.
D. 0,86.
Tỉ lệ học sinh bị cận thị ở một trường trung học cơ sở là \(16\% \). Gặp ngẫu nhiên một học sinh của trường, xác suất học sinh đó không bị cận thị là
A. 0,16.
B. 0,94.
C. 0,84.
D. 0,5.
Tỉ lệ vận động viên đạt huy chương trong một đại hội thể thao là 21%. Gặp ngẫu nhiên một vận động viên dự đại hội. Tính xác suất của biến cố vận động viên ấy đạt huy chương.
Thảo tung hai đồng xu giống nhau 100 lần và ghi lại kết quả ở bảng sau:

Tính xác suất thực nghiệm của biến cố “Hai đồng xu đều xuất hiện mặt sấp sau 100 lần tung”.
Nếu tung một đồng xu 40 lần liên tiếp, có 19 lần xuất hiện mặt N thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” bằng bao nhiêu?
Gieo xúc xắc 30 lần liên tiếp, có 4 lần xuất hiện mặt 2 chấm. Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 2 chấm”.
Mỗi hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số nguyên dương không vượt quá 10, hai thẻ khác nhau thì ghi hai số khác nhau. Lấy ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp. Sau 40 lần lấy thẻ liên tiếp, thẻ ghi số 1 được lấy ra 3 lần. Tính xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số 1” trong trò chơi trên.
Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” trong mỗi trường hợp sau:
a) Tung một đồng xu 50 lần liên tiếp, có 27 lần xuất hiện mặt S;
b) Tung một đồng xu 45 lần liên tiếp, có 24 lần xuất hiện mặt N.
Gieo một xúc xắc 30 lần liên tiếp, ghi lại mặt xuất hiện của xúc xắc sau mỗi lần gieo. Tính xác suất thực nghiệm của mỗi biến cố sau:
a) “Mặt xuất hiện của xúc xắc là mặt 3 chấm”;
b) “Mặt xuất hiện của xúc xắc là mặt 4 chấm”
Trong đợt phát động “Hiến máu cứu người- Cần lắm những tấm lòng”, có rất nhiều sinh viên thuộc các trường đại học ở Thành phố Hồ Chí Minh tình nguyện hiến máu.
Nhóm máu của \(300\) sinh viên đến trước được thống kê trong Bảng 7.9 dưới đây:

Chọn ngẫu nhiên một sinh viên trong số này. Tính xác suất thực nghiệm của biến cố “chọn được người có nhóm máu AB” trong số \(300\) sinh viên.
Mỗi xạ thủ muốn tham gia một cuộc thi nào đó đều phải luyện tập rất nhiều. Trong những lần luyện tập cuối, anh Hoàng thấy cứ bắn \(150\) viên đạn thì có khoảng từ \(138\) đến \(142\) viên trúng tâm bia.
a) Hỏi xác suất thực nghiệm bắn trúng tâm bia của anh Hoàng trong những lần tập luyện cuối xấp xỉ bằng bao nhiêu?
b) Từ kết quả tập luyện, hãy ước lượng xác suất bắn đạn trúng tâm bia của anh Hoàng.
Trong hộp có một số bút chì. Bảo rút ngẫu nhiên một bút, ghi lại màu của nó rồi bỏ lại vào hộp, và tiếp tục rút lần khác. Sau \(10\) lần thực hiện thí nghiệm này, Bảo rút được \(6\) bút đỏ và \(4\) bút xanh. Bảo kết luận: “Xác suất lấy được bút vàng bằng \(0,\) suy ra trong hộp không có bút màu vàng”. Em có đồng ý với ý kiến của Bảo không? Vì sao?
Anh Quang, một sinh viên y khoa, đã tiến hành tìm hiểu tác hại của thuốc lá đối với sức khỏe con người. Anh rút ngẫu nhiên \(500\) hồ sơ bệnh nhân ung thư phổi đang điều trị ở một số bệnh viện để nghiên cứu. Trong \(500\) hồ sơ rút ra, anh Quang thấy có \(442\) người đã từng nghiện thuốc lá.
a) Đối với hoạt động chọn ngẫu nhiên \(500\) bệnh nhân ung thư phổi mà anh Quang đã thực hiện, hãy tính xác suất thực nghiệm của các biến cố:
A: “Chọn đúng người có hút thuốc lá”;
B: “Chọn đúng người không hút thuốc lá”.
b) Hòa nói: “Nếu tiếp tục chọn thêm một người nữa trong số các bệnh nhân ung thư, chắc chắn là anh Quang sẽ chọn được người hút thuốc”.
Thuận nói: “Chưa chắc. Nhưng khả năng chọn cao hơn rất nhiều, gấp hơn khoảng \(9\) lần so với khả năng chọn được người không hút thuốc”.
Em đồng ý với ý kiến nào? Vì sao?
Anh Phúc đã khảo sát thời lượng quảng cáo trên ti vi (tính bằng giây) qua một số buổi phát lấy ngẫu nhiên và biểu diễn kết quả khảo sát bằng biểu đồ dưới đây:
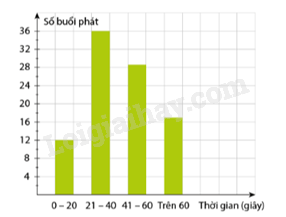
Ước tính xác suất (lấy đến một chữ số thập phân) để tối hôm sau chương trình anh Phúc mở ra xem có thời gian quảng cáo kéo dài:
a) Từ \(21\) đến \(40\) giây;
b) Từ \(21\) đến \(60\) giây;
c) Trên một phút.
Bạn Nam tung một đồng xu cân đối và đồng chất 20 lần, có 13 lần mặt ngửa. Xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là
Trong hộp bút của bạn Hoa có 5 bút bi xanh, 3 bút bi đỏ và 2 bút bi đen. Xác suất thực nghiệm của biến cố “Bạn Hoa lấy một bút bi đỏ” là
Trong hộp bút của bạn Hoa có 5 bút bi xanh, 3 bút bi đỏ và 2 bút bi đen. Xác suất thực nghiệm của biến cố “Bạn Hoa lấy một bút bi đỏ” là:
Một đội thanh niên tình nguyện gồm 11 thành viên đến từ các tỉnh, TP như sau: Kon Tum; Bình Phước; Tây Ninh; Bình Dương; Gia Lai; Bà Rịa – Vũng Tàu; Đồng Nai; Đăk Lăk ; Đăk Nông; Lâm Đồng; TP Hồ Chí Minh, mỗi tỉnh, TP chỉ có đúng một thành viên trong đội. Chọn ngẫu nhiên một thành viên của đội tình nguyện đó.
a) Gọi K là tập hợp gồm các kết quả có thể xảy ra đối với thành viên được chọn. Tính số phần tử của tập hợp K.
b) Tính xác suất của mỗi biến cố sau :
− “Thành viên được chọn ra đến từ vùng Tây Nguyên”.
− “Thành viên được chọn ra đến từ vùng Đông Nam Bộ”.

Gieo 90 lần một con xúc xắc cân đối và đồng chất ta được kết quả như sau:

Xác suất thực nghiệm của sự kiện gieo được mặt có số chấm nhỏ hơn 3 là:
Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S” trong mỗi trường hợp sau:
a) Tung một đồng xu 25 lần liên tiếp, có 29 lần xuất hiện mặt S;
b) Tung một đồng xu 32 lần liên tiếp, có 17 lần xuất hiện mặt N.






