Cho tam giác ABC vuông tại A có AB < AC , đường cao AH . Gọi I là trung điểm của AB. Lấy K đối xứng với B qua H . Qua A kẻ đường thẳng song song với BC , cắt HI tại D.

a) Chứng minh AD = BH . Từ đó chứng minh tứ giác AKHD là hình bình hành;

b) Chứng minh tứ giác AHBD là hình chữ nhật. Tính diện tích AHBD nếu AH = 6 cm, BH = 8cm;

c) Tam giác ABC cần có thêm điều kiện gì đề tứ giác AHBD là hình vuông?

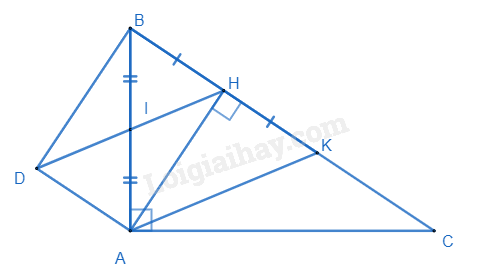
a) Vì AD // BC nên ta có \(\widehat {DAB} = \widehat {HBA}\) (hai góc so le trong).

Xét tam giác ADI và tam giác BHI có:

\(\widehat {DAB} = \widehat {HBA}\) (cmt)

AI = BI (I là trung điểm của AB)

\(\widehat {AID} = \widehat {BIH}\)

nên \(\Delta ADI = \Delta BHI\).

Suy ra DI = IH, AH = BH (đpcm).

Vì K đối xứng với B qua H nên BH = HK.

Xét tứ giác AKHD có:

AD // HK (vì AD // BC)

AD = HK (cùng = BH)

Nên AKHD là hình bình hành (vì có cặp cạnh đối song song và bằng nhau).

b) Xét tứ giác AHBD có

AI = BI = \(\frac{1}{2}\)AB

DI = HI = \(\frac{1}{2}\)DH

AB \( \cap \) DH = I

nên tứ giác AHBD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

Ta lại có \(\widehat {AHB} = {90^0}\) nên AHBD là hình chữ nhật (vì hình bình hành có một góc vuông là hình chữ nhật).

c) Để AHBD là hình vuông thì AH = BH. Mà \(\widehat {AHB} = {90^0}\) nên tam giác AHB phải là tam giác vuông cân tại H.

Khi tam giác AHB vuông cân thì \(\widehat {ABH} = \widehat {BAH} = {45^0}\).

Mà tam giác ABC vuông tại A => \(\widehat C = {180^0} - {90^0} - {45^0} = {45^0}\) hay tam giác ABC vuông cân tại A.

Vậy để AHBD là hình vuông thì ABC phải là tam giác vuông cân tại A.