Tìm \(m\) để các hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{\sqrt[3]{{x - 2}} + 2x - 1}}{{x - 1}}{\rm{ khi }}x \ne 1\\3m - 2{\rm{ khi }}x = 1\end{array} \right.\) liên tục trên \(\mathbb{R}\).
-
A.
\(m = \frac{13}{9}\)
-
B.
\(m = \frac{5}{3}\)
-
C.
\(m = \frac{3}{4}\)
-
D.
\(m = 0\)
Hàm số \(y = \left\{ \begin{array}{l}f(x){\rm{ khi }}x \ne {x_0}\\k{\rm{ khi }}x = {x_0}\end{array} \right.\) liên tục tại \(x = {x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f(x) = k\).
Hàm số liên tục trên tập xác định.
Với \(x \ne 1\) ta có \(f\left( x \right) = \frac{{\sqrt[3]{{x - 2}} + 2x - 1}}{{x - 1}}\) nên hàm số liên tục trên khoảng \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Do đó hàm số liên tục trên \(\mathbb{R}\) khi và chỉ khi hàm số liên tục tại \(x = 1\).
Ta có: \(f\left( 1 \right) = 3m - 2\).
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[3]{{x - 2}} + 2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left[ {1 + \frac{{{x^3} + x - 2}}{{\left( {x - 1} \right)\left( {{x^2} - x\sqrt[3]{{x - 2}} + \sqrt[3]{{{{(x - 2)}^2}}}} \right)}}} \right]\\ = \mathop {\lim }\limits_{x \to 1} \left[ {1 + \frac{{{x^2} + x + 2}}{{{x^2} - x\sqrt[3]{{x - 2}} + \sqrt[3]{{{{\left( {x - 2} \right)}^2}}}}}} \right] = \frac{7}{3}.\end{array}\)
Nên hàm số liên tục tại \(x = 1 \Leftrightarrow 3m - 2 = \frac{7}{3} \Leftrightarrow m = \frac{13}{9}\).
Vậy \(m = \frac{13}{9}\) là những giá trị cần tìm.
Đáp án : A
Các bài tập cùng chuyên đề
Tìm các khoảng trên đó hàm số \(f\left( x \right) = \frac{{{x^2} + 1}}{{x + 2}}\) liên tục.
Cho hai hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{2x\;,\;0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\) và \(g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x\;,0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\)với đồ thị tương ứng như Hình 5.7
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm \(x = \frac{1}{2}\)và nhận xét về sự khác nhau giữa hai đồ thị.
Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
a) \(f\left( x \right) = \frac{x}{{{x^2} + 5x + 6}}\)
b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{1 + {x^2}\;,\;x < 1}\\{4 - x\;\;,\;x \ge 1}\end{array}} \right.\)
Cho hàm số \(f\left( x \right) = \frac{{x + 1}}{{\left| {x + 1} \right|}}\). Hàm só \(f\left( x \right)\) liên tục trên
A. \(\left( { - \infty ;\; + \infty } \right)\)
B. \(\left( { - \infty ;\; - 1} \right]\)
C. \(\left( { - \infty ;\; - 1} \right) \cup \left( { - 1;\; + \infty } \right)\)
D. \(\left[ { - 1;\; + \infty } \right)\)
Tìm tập xác định của các hàm số sau và giải thích tại sao các hàm này liên tục trên các khoảng xác định của chúng
a) \(f\left( x \right) = \frac{{\cos x}}{{{x^2} + 5x + 6}}\);
b) \(g\left( x \right) = \frac{{x - 2}}{{\sin x}}\)
Lực hấp dẫn tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm Trái Đất là
\(F\left( r \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{GMr}}{{{R^3}}}\;,r < R}\\{\frac{{GM}}{{{r^2}}}\;,\;r \ge R}\end{array}} \right.\)
Trong đó M và R lần lượt là khối lượng và bán kính của Trái Đất, G là hằng số hấp dẫn. Xét tính liên tục của hàm số F(r).
Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x - 1,\,\,x < 2\\ - x,\,\,x \ge 2\end{array} \right.\) có liên tục trên \(\mathbb{R}\) hay không?
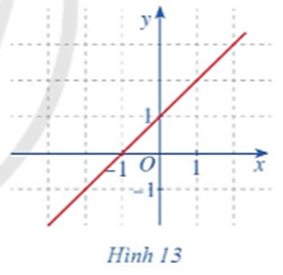
Cho hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}.\)
a) Giả sử \({x_0} \in \mathbb{R}.\) Hàm số \(f\left( x \right)\) có liên tục tại điểm \({x_0}\) hay không?
b) Quan sát đồ thị hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}\) (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
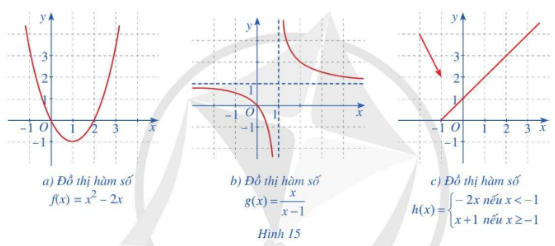
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
a) \(f\left( x \right) = {x^2} + \sin x;\)
b) \(g\left( x \right) = {x^4} - {x^2} + \frac{6}{{x - 1}};\)
c) \(h\left( x \right) = \frac{{2x}}{{x - 3}} + \frac{{x - 1}}{{x + 4}}.\)
Tại một xưởng sản xuất bột đã thạch anh, giá bán (tính theo nghìn đồng) của \(x\) (kg) bột đã thạch anh được tính theo công thức sau:
\(P\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{4,5x}&{khi\,\,0 < x \le 400}\\{4x + k}&{khi\,\,x > 400}\end{array}} \right.\) (\(k\) là một hãng số).
a) Với \(k = 0\), xét tính liên tục của hàm số \(P\left( x \right)\) trên \(\left( {0; + \infty } \right)\).
b) Với giá trị nào của \(k\) thì hàm số \(P\left( x \right)\) liên tục trên \(\left( {0; + \infty } \right)\)?
Xét tính liên tục của hàm số \(y = \sqrt {x - 1} + \sqrt {2 - x} \) trên \(\left[ {1;2} \right]\).
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1}&{khi\,\,1 < x \le 2}\\k&{khi\,\,x = 1}\end{array}} \right.\).
a) Xét tính liên tục của hàm số tại mỗi điểm \({x_0} \in \left( {1;2} \right)\).
b) Tìm \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)\) và so sánh giá trị này với \(f\left( 2 \right)\).
c) Với giá trị nào của \(k\) thì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = k\)?
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 4}}{{x + 2}}}&{khi\,\,x \ne - 2}\\a&{khi\,\,x = - 2}\end{array}} \right.\).
Tìm \(a\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Xét tính liên tục của các hàm số sau:
a) \(f\left( x \right) = \frac{x}{{{x^2} - 4}}\);
b) \(g\left( x \right) = \sqrt {9 - {x^2}} \);
c) \(h\left( x \right) = \cos x + \tan x\).
Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\sqrt {x + 4} }&{khi\,\,x \ge 0}\\{2\cos x}&{khi\,\,x < 0}\end{array}} \right.\).
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 25}}{{x - 5}}}&{khi\,\,x \ne 5}\\a&{khi\,\,x = 5}\end{array}} \right.\).
Tìm \(a\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\tan x\;\;\;\;\;\;\,khi\;0 < x \le \frac{\pi }{4}\\k - \cot x\;\,khi\;\frac{\pi }{4} < x \le \frac{\pi }{2}\end{array} \right.\) liên tục tại trên đoạn \(\left[ {0;\frac{\pi }{2}} \right]\). Giá trị của k bằng
A. 0.
B. 1.
C. 2.
D. \(\frac{\pi }{2}\).
Hàm số \(y = f\left( x \right)\) liên tục trên khoảng:
A. \(\left( { - \infty ;1} \right)\)
B. \(\left( { - \infty ; + \infty } \right)\)
C. \(\left( {1; + \infty } \right)\)
D. \(\left( { - \infty ;2} \right)\)
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3\;\;\;\;\;\;\;\;\;khi\;x \le 1\\ax + b\;\;khi\;1 < x < 2\\5\;\;\;\;\;\;\;\;\;khi\;x \ge 2\end{array} \right.\). Xác định a, b để hàm số liên tục trên \(\mathbb{R}\).
Tìm tham số m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\;\;\;khi\;x < 1\\mx + 1\;\;khi\;x \ge 1\end{array} \right.\) liên tục trên \(\mathbb{R}\).
Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
a) \(f\left( x \right) = \frac{{{x^3} + x + 1}}{{{x^2} - 3x + 2}}\)
b) \(f\left( x \right) = \frac{{\cos x}}{{{x^2} + 3x - 4}}\)
Cho hàm số \(f(x) = \left\{ \begin{array}{l}2\,\,\,{\rm{khi}}\,\,\, - 1 < x \le 1\\1 - x\,\,{\rm{khi}}\,\,x \le - 1\,\,{\rm{hay}}\,\,x > 1\end{array} \right.\). Mệnh đề đúng là
A. Hàm số \(f(x)\) liên tục trên \([ - 1;\,1]\)
B. Hàm số \(f(x)\) liên tục trên \(( - 1;\,1]\)
C. Hàm số \(f(x)\) liên tục trên \([ - 1;\,1)\)
D. Hàm số \(f(x)\) liên tục trên \(\mathbb{R}\).
Xét hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} + 3x + 2}}{{x + 1}}\,\,{\rm{khi}}\,\,x \ne - 1\\m\,\,{\rm{khi}}\,\,\,x = - 1\end{array} \right.\) với m là tham số. Hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) khi
A. \(m = 0\)
B.\(m = 3\)
C.\(m = - 1\)
D.\(m = 1\).
Cho hàm số \(f(x) = \frac{{x(x - 1)}}{{\sqrt {x - 1} }}\). Hàm số này liên tục trên
A.\(\left( {1; + \infty } \right)\)
B.\(\left( { - \infty ;1} \right)\)
C. \([1; + \infty )\)
D. \(( - \infty ;1]\).
Cho các hàm số \(y = \cos x\,\left( I \right)\), \(y = \sin \sqrt x \,\left( {II} \right)\) và \(y = \tan x\,\left( {III} \right)\). Hàm số nào liên tục trên \(\mathbb{R}\)?
Tìm khẳng định đúng trong các khẳng định sau:
I. \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f\left( a \right) \cdot f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có nghiệm.
II. \(f\left( x \right)\) không liên tục trên \(\left[ {a;b} \right]\) và \(f\left( a \right) \cdot f\left( b \right) \ge 0\) thì phương trình \(f\left( x \right) = 0\) vô nghiệm.
Hàm số nào sau đây liên tục trên \(\mathbb{R}?\)
Hàm số nào sau đây liên tục trên $\mathbb{R}$?
Cho hàm số $y = f\left( x \right)$ liên tục trên $\left( {a;b} \right)$. Điều kiện cần và đủ để hàm số liên tục trên $\left[ {a;b} \right]$ là
