Rút gọn \(S = 1 + {\cos ^2}x + {\cos ^4}x + {\cos ^6}x + .... + {\cos ^{2n}}x + ...\) với \(\cos x \ne \pm 1\).
-
A.
\(S = {\sin ^2}x\)
-
B.
\(S = {\cos ^2}x\)
-
C.
\(S = \frac{1}{{\sin^2 x}}\)
-
D.
\(S = \frac{1}{{{{\cos }^2}x}}\)
Nhận biết đây là tổng của một cấp số nhân.
Khi đó tổng \({S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\).
Vì \( - 1 \le \cos x \le 1,\,\cos x \ne \pm 1 \Rightarrow - 1 < \cos x < 1\).
Do đó \(1,\,{\cos ^2}x,{\cos ^4}x,{\cos ^6}x,....,{\cos ^{2n}}x,...\) là cấp số nhân lùi vô hạn với công bội \(q ={\cos ^2}x\).
Do đó:
\(S = 1 + {\cos ^2}x + {\cos ^4}x + {\cos ^6}x + .... + {\cos ^{2n}}x + ... = \frac{1}{{1 - {{\cos }^2}x}} = \frac{1}{{{{\sin }^2}x}}\).
Đáp án : C

Các bài tập cùng chuyên đề
Để đơn giản, ta giả sử Achilles chạy với vận tốc 100km.h, vận tốc của rùa là 1 km/h và khoảng cách ban đầu a = 100(km)
a) Tính thời gian \({t_1},\;{t_2}, \ldots ,{t_n}, \ldots \) tương ứng để Achilles đi từ \({A_1}\) đến \({A_2}\), từ \({A_2}\) đến \({A_3}\),…, từ \({A_n}\) đến \({A_{n + 1}}\),…
b) Tính tổng thời gian cần thiết để Achilles chạy hết các quãng đường \({A_1}{A_2},\;{A_2}{A_3}, \ldots ,\;{A_n}{A_{n + 1}}\),… tức là thời gian cần thiết để Achilles đuổi kịp rùa
c) Sai lầm trong lập luận của Zeno là ở đâu?
Tính tổng \(S = 2 + \frac{2}{7} + \frac{2}{{7^2}} + \ldots + \frac{2}{{{7^{n - 1}}}} + \ldots \).
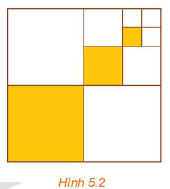
Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau, sau đó ô màu hình vuông nhỏ góc dưới bên trái (H.5.2). Lặp lại các thao tác này với hình vuông nhỏ góc trên bên phải. Giả sử quá trình trên tiếp diễn vô hạn lần. Gọi \({u_1},\;{u_2}, \ldots ,\;{u_n}, \ldots \) lần lượt là độ dài cạnh của các hình vuông được tô màu.
a) Tính tổng \({S_n} = {u_1} + {u_2} + \ldots + {u_n}\)
b) Tìm \(S = \mathop {lim}\limits_{n \to + \infty } {S_n}\)
Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số
a) 1, (12) = 1, 121212…; b) 3, (102) = 3, 102102102…
Cho cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với \({u_n} = \frac{2}{{{3^n}}}\). Tổng của cấp số nhân này bằng
A. 3
B. 2
C. 1
D. 6
Giải thích vì sao nghịch lí Zénon trong phần mở đầu là không đúng trong trường hợp sau: Giả sử tốc độ chạy của Achilles là 100km/h, còn tốc độ chạy của rùa là 1km/h. Lúc xuất phát rùa ở điểm \(A_1\) cách Achilles 100km.
Tính tổng \(M = 1 - \frac{1}{2} + \frac{1}{{{2^2}}} - ... + {\left( { - \frac{1}{2}} \right)^{n - 1}} + ...\)
Cho cấp số nhân \(\left( {{u_n}} \right),\) với \({u_1} = 1\) và công bội \(q = \frac{1}{2}.\)
a) So sánh \(\left| q \right|\) với 1.
b) Tính \({S_n} = {u_1} + {u_2} + ... + {u_n}.\) Từ đó, hãy tính \(\lim {S_n}.\)
a) Tính tổng của cấp số nhân lùi vô hạn \(\left( {{u_n}} \right),\) với \({u_1} = \frac{2}{3},q = - \frac{1}{4}.\)
b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số.
Từ tờ giấy, cắt một hình tròn bán kính \(R\left( {cm} \right)\) như Hình 3a. Tiếp theo, cắt hai hình tròn bán kính \(\frac{R}{2}\) rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính \(\frac{R}{4}\) rồi chồng lên các hình trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn.

Tính tổng của cấp số nhân lùi vô hạn: \(1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + ... + {\left( {\frac{1}{3}} \right)^n} + ...\).
Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa hình còn lại và cứ tiếp tục như vậy (xem Hình 2).
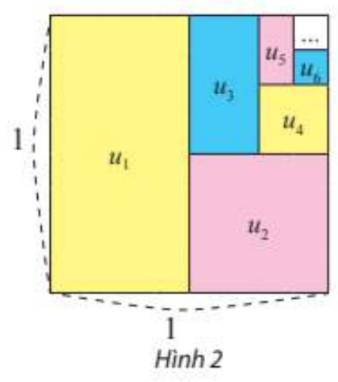
a) Xác định diện tích \({u_k}\) của phần hình được tô màu lần thứ \(k\left( {k = 1,2,3,...} \right)\).
b) Tính tổng diện tính \({S_n}\) của phần hình được tô màu sau lần tô thứ \(n\left( {n = 1,2,3,...} \right)\).
c) Tìm giới hạn \(\lim {S_n}\) và so sánh giới hạn này với diện tích hình vuông ban đầu.
Tính tổng của các cấp số nhân lùi vô hạn sau:
a) \( - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + ... + {\left( { - \frac{1}{2}} \right)^n} + ...\)
b) \(\frac{1}{4} + \frac{1}{{16}} + \frac{1}{{64}} + ... + {\left( {\frac{1}{4}} \right)^n} + ...\)
Viết số thập phân vô hạn tuần hoàn \(0,444...\) dưới dạng một phân số.
Tổng của cấp số nhân lùi vô hạn: \(M = 1 + \frac{1}{4} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{4^n}}} + ...\) bằng:
A. \(\frac{3}{4}\).
B. \(\frac{5}{4}\).
C. \(\frac{4}{3}\).
D. \(\frac{6}{5}\).
Viết các số thập phân vô hạn tuần hoàn sau thành phân số:
a) \(0,\left( 7 \right) = 0,777...\);
b) \(1,\left( {45} \right) = 1,454545...\)
Tính tổng của các cấp số nhân lùi vô hạn:
a) \(1 - \frac{1}{5} + \frac{1}{{{5^2}}} - \frac{1}{{{5^3}}} + ... + {\left( { - \frac{1}{5}} \right)^n} + ...\)
b) \(2 + \frac{{{2^2}}}{3} + \frac{{{2^3}}}{{{3^2}}} + ... + \frac{{{2^n}}}{{{3^{n - 1}}}} + ...\)
Tại một nhà máy, người ta đo được rằng 80% lượng nước sau khi sử dụng được xử lí và tái sử dụng. Với \(100{m^3}\) ban đầu được sử dụng lần đầu tại nhà máy, khi quá trình xử lí và tái sử dụng lặp lại mãi mãi, nhà máy sử dụng được tổng lượng nước là bao nhiêu?
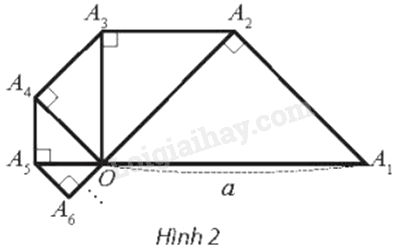
Tam giác \(O{A_1}{A_2}\) vuông cân tại \({A_2}\) có cạnh huyền \(O{A_1}\) bằng a. Bên ngoài tam giác \(O{A_1}{A_2}\), vẽ tam giác \(O{A_2}{A_3}\) vuông cân tại \({A_3}\). Tiếp theo, bên ngoài tam giác \(O{A_2}{A_3}\), vẽ tam giác \(O{A_3}{A_4}\) vuông cân tại \({A_4}\). Cứ tiếp tục quá trình như trên, ta vẽ được một dãy các hình tam giác vuông cân (Hình 2). Tính độ dài đường gấp khúc \({A_1}{A_2}{A_3}{A_4}...\)
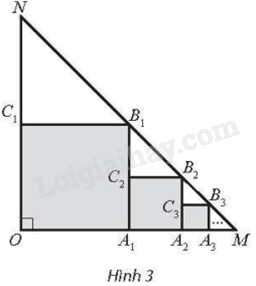
Cho tam giác OMN vuông cân tại O, \(OM = ON = 1\). Trong tam giác OMN, vẽ hình vuông \(O{A_1}{B_1}{C_1}\) sao cho các đỉnh \({A_1},{B_1},{C_1}\) lần lượt nằm trên các cạnh OM, MN, ON. Trong tam giác \({A_1}M{B_1}\), vẽ hình vuông \({A_1}{A_2}{B_2}{C_2}\) sao cho các đỉnh \({A_2},{B_2},{C_2}\) lần lượt nằm trên các cạnh \({A_1}M,M{B_1},{A_1}{B_1}\). Tiếp tục quá trình đó, ta được một dãy các hình vuông (Hình 3). Tính tổng diện tích các hình vuông này.
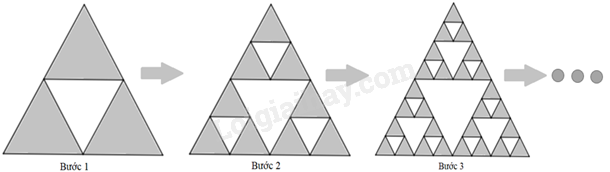
Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau:
Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích \(\frac{1}{4}\)).
Bước 2: Làm tương tự bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác, mỗi tam giác có diện tích \(\frac{1}{{{4^2}}}\))
Cứ tiếp tục quá trình như vậy (ở bước thứ n, bỏ đi \({3^{n - 1}}\) tam giác, mỗi tam giác có diện tích \(\frac{1}{{{4^n}}}\)). Tính tổng diện tích các tam giác đã bỏ đi.
Biết rằng, từ vị trí A, một mũi tên bay với tốc độ 10m/s hướng thẳng tới bia mục tiêu đặt ở vị trí B cách vị trí A một khoảng bằng 10m (Hình 2). Một nhà thông thái lập luận như sau: “Để đến được B, trước hết mũi tên phải đến trung điểm \({A_1}\) của AB. Tiếp theo, nó phải đến trung điểm \({A_2}\) của \({A_1}B\). Tiếp nữa, nó phải đi đến trung điểm \({A_3}\) của \({A_2}B\). Cứ tiếp tục như vậy, vì không bao giờ hết các trung điểm nên mũi tên không thể đến được mục tiêu ở B”.

Lập luận trên có đúng không? Nếu không, hãy chỉ chỗ ra sai lầm.
a) Tính tổng của cấp số nhân lùi vô hạn \(\left( {{u_n}} \right)\) với \({u_1} = \frac{5}{4}\), \(q = - \frac{1}{3}\).
b) Biểu diễn số thập phân vô hạn tuần hoàn \(2,\left( 3 \right)\) dưới dạng phân số.
Biểu diễn dưới dạng phân số của \(1,\left( 7 \right)\) là:
A. \(\frac{7}{9}\)
B. \(\frac{{10}}{9}\)
C. \(\frac{{10}}{3}\)
D. \(\frac{{16}}{9}\)
Cho tam giác \({T_1}\) có diện tích bằng 1. Giả sử có tam giác \({T_2}\) đồng dạng với tam giác \({T_1}\), tam giác \({T_3}\) đồng dạng với tam giác \({T_2}\), …, tam giác \({T_n}\) đồng dạng với tam giác \({T_{n - 1}}\) với tỉ số đồng dạng \(\frac{1}{k}{\rm{ }}\left( {k > 1} \right)\). Khi \(n\) tiến tới vô cùng, tính tổng diện tích của tất cả các tam giác theo \(k\).
Tính tổng \(S = - 1 + \frac{1}{5} - \frac{1}{{{5^2}}} + ... + {\left( { - 1} \right)^n}\frac{1}{{{5^{n - 1}}}} + ...\).
Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:
a) 1,(03);
b) 3,(23).
Cho tam giác \({A_1}{B_1}{C_1}\) có diện tích là 3 (đơn vị diện tích). Dựng tam giác \({A_2}{B_2}{C_2}\) bằng cách nối các trung điểm của các cạnh \({B_1}{C_1},{C_1}{A_1},{A_1}{B_1}.\) Tiếp tục quá trình này, ta có các tam giác \({A_3}{B_3}{C_3},...,{A_n}{B_n}{C_n},...\) Kí hiệu \({s_n}\) là diện tích của tam giác \({A_n}{B_n}{C_n}\).
a) Tính \({s_n}\).
b) Tính tổng \({s_1} + {s_2} + ... + {s_n} + ...\).
Tính tổng \(S = - \frac{2}{3} + \frac{2}{9} - \frac{2}{{27}} + ... + {( - 1)^n}.\frac{2}{{{3^n}}} + ...\)
A. \(S = \frac{1}{2}\)
B.\(S = - \frac{1}{2}\)
C.\(S = - 3\)
D. \(S = 3\).
Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:
a) \( - 0,(31)\)
b) \(2,(121)\)







Danh sách bình luận