-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Câu hỏi tự luyện Toán 11
-
TẢI 50 ĐỀ KIỂM TRA 15 PHÚT TOÁN 11
-
TẢI 30 ĐỀ KIỂM TRA 1 TIẾT TOÁN 11
-
TẢI 5 ĐỀ THI GIỮA KÌ 1 TOÁN 11
-
TẢI 25 ĐỀ THI HỌC KÌ 1 TOÁN 11
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 11
-
TẢI 20 ĐỀ THI HỌC KÌ 2 TOÁN 11
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Bài 1. Giới hạn của dãy số
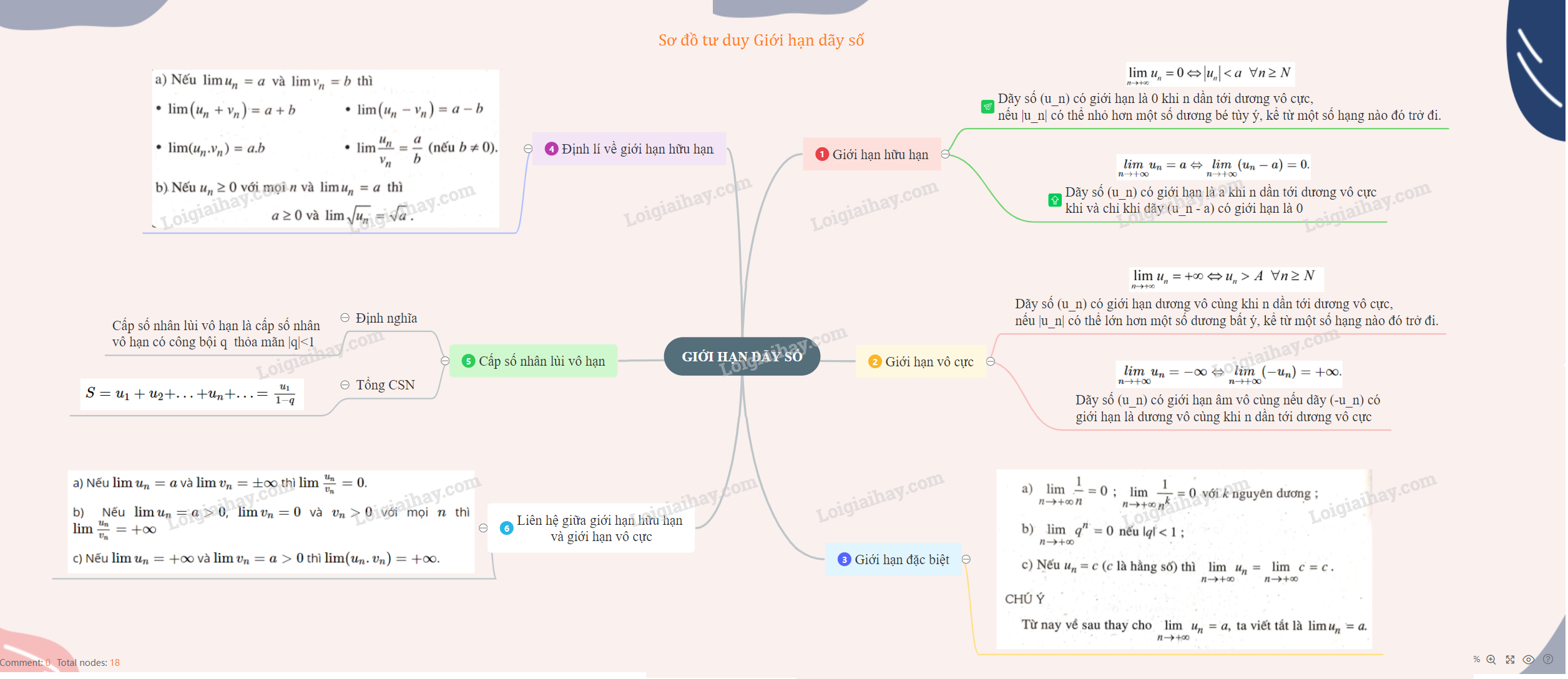
Lý thuyết về giới hạn của dãy số
Cấp số nhân lùi vô hạn là cấp số nhân vô hạn có công bội q thỏa mãn |q|
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
1. Giới hạn hữu hạn
+) \(\underset{n\rightarrow +\infty }{lim }u_{n} = 0\) khi và chỉ khi \(|u_n|\) có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
+) \(\underset{n\rightarrow +\infty }{lim }u_{n} = a \Leftrightarrow \underset{n\rightarrow +\infty }{lim }(u_{n}-a) = 0\).
2. Giới hạn vô cực
+) \(\underset{n\rightarrow +\infty }{lim }u_{n}= +∞\) khi và chỉ khi \(u_n\) có thể lớn hơn một số dương tùy ý, kể từ một số hạng nào đó trở đi.
+ \(\underset{n\rightarrow +\infty }{lim }u_{n} = -∞ \Leftrightarrow \underset{n\rightarrow +\infty }{lim}(-u_{n})= +∞\).
3. Các giới hạn đặc biệt
a) \(\lim \frac{1}{n} = 0\);
\(\lim \frac{1}{n^{k}} = 0\);
\(\lim n^k= +∞\), với \(k\) nguyên dương.
b) \(\lim q^n= 0\) nếu \(|q| < 1\);
\(\lim q^n= +∞\) nếu \(q > 1\).
c) \(\lim c = c\) (\(c\) là hằng số).
4. Định lí về giới hạn hữu hạn
a) Nếu \(\lim u_n=a\) và \(\lim v_n= b\), thì:
\(lim\left( {{u_{n}}+{v_n}} \right)= a +b\)
\(lim{\rm{ }}({u_n} - {v_n}){\rm{ }} = {\rm{ }}a - b\)
\(lim{\rm{ }}({u_n}.{v_n}) = ab\)
\(lim{{{u_n}} \over {{v_n}}} = {a \over b}\) (nếu \(b ≠ 0\)).
b) Nếu \(u_n≥ 0\) với mọi \(n\) và \(lim u_n= a\) thì \(a > 0\) và \(lim \sqrt{u_n}= \sqrt a\).
5. Định lí liên hệ giữa giới hạn hữu hạn và giới hạn vô cực.
a) Nếu \(\lim u_n=a\) và \(\lim v_n= ± ∞\) thì \(\lim \frac{u_{n}}{v_{n}}= 0\).
b) Nếu \(\lim u_n=a > 0\), \(\lim v_n= 0\) và \(v_n> 0\) với mọi \(n\) thì \(\lim \frac{u_{n}}{v_{n}} = +∞\)
c) Nếu \(\lim u_n= +∞\) và \(\lim v_n= a > 0\) thì \(\lim (u_n.v_n) = +∞\).
6. Cấp số nhân lùi vô hạn
+ Cấp số nhân lùi vô hạn là cấp số nhân vô hạn có công bội \(q\) thỏa mãn \(|q| <1\).
+) Công thức tính tổng \(S\) của cấp số lùi vô hạn \((u_n)\):
\(S = {u_1} + {u_2} + ... + {u_n} + ... = {{{u_1}} \over {1 - q}}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu hỏi 1 trang 112 SGK Đại số và Giải tích 11
- Câu hỏi 2 trang 117 SGK Đại số và Giải tích 11
- Bài 1 trang 121 SGK Đại số và Giải tích 11
- Bài 2 trang 121 SGK Đại số và Giải tích 11
- Bài 3 trang 121 SGK Đại số và Giải tích 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
