Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Bài 4. Hai mặt phẳng vuông góc

Bài 3 trang 113 SGK Hình học 11


Trong mặt phẳng

Đề bài

Trong mặt phẳng \((\alpha)\) cho tam giác \(ABC\) vuông ở \(B\). Một đoạn thẳng \(AD\) vuông góc với \((\alpha)\) tại \(A\). Chứng minh rằng:

a) \(\widehat {ABD}\) là góc giữa hai mặt phẳng \((ABC)\) và \((DBC)\);

b) Mặt phẳng \((ABD)\) vuông góc với mặt phẳng \((BCD)\);

c) \(HK//BC\) với \(H\) và \(K\) lần lượt là giao điểm của \(DB\) và \(DC\) với mặt phẳng \((P)\) đi qua \(A\) và vuông góc với \(DB\).

Video hướng dẫn giải

Lời giải chi tiết

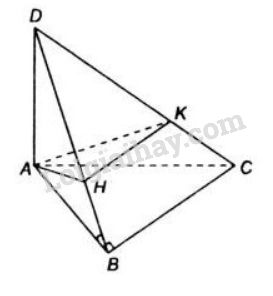
a) Tam giác \(ABC\) vuông tại \(B\) nên \(AB \, \bot \, BC\) (1)

\(AD\) vuông góc với \((\alpha)\) nên \(AD \, \bot \, BC\) (2)

Từ (1) và (2) suy ra \(BC \, \bot \, (ABD)\) suy ra \(BC \, \bot \, BD\)

\(\left. \matrix{
(ABC) \cap (DBC) = BC \hfill \cr
BD \, \bot \, BC \hfill \cr
AB \,\bot \, BC \hfill \cr} \right\} \)

\(\Rightarrow \) góc giữa hai mặt phẳng \((ABC)\) và \((DBC)\) là góc giữa hai đường thẳng \(BD\) và \(BA\)

Mà \(DA \, \bot \, \left( {ABC} \right) \Rightarrow DA \, \bot \, AB\) \( \Rightarrow \widehat {ABD} < {90^0}\)

Vậy \(\widehat {ABD}\) là góc giữa hai mặt phẳng \((ABC)\) và \((DBC)\).

b)

\(\left. \matrix{
BC\, \bot \, (ABD) \hfill \cr
BC \, \subset \, (BCD) \hfill \cr} \right\}\) \( \Rightarrow (ABD) \, \bot \, (BCD)\)

c) Do \((P)\) đi qua \(A, H, K\) nên mặt phẳng \(\left( P \right) \equiv \left( {AHK} \right)\) đi qua \(A\) và vuông góc với \(DB\) nên \(HK\bot BD\)

Trong \((BCD)\) có: \(HK \, \bot \, BD\) và \(BC \, \bot \, BD\) nên suy ra \(HK \, // \,BC\).

Chú ý:

Từ chứng minh trên ta có thể suy ra cách dựng \((P)\) như sau:

Trong \((DAB),\) qua \(A\) kẻ đường thẳng vuông góc với \(DB\) cắt \(DB\) tại \(H.\)

Trong \((DBC)\), kẻ đường thẳng qua \(H\) và vuông góc với \(DB\) cắt \(DC\) tại \(K.\)

Từ đó ta có \((P)\) chính là \((AHK).\)

Loigiaihay.com


Bình chọn:
3.6 trên 14 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store