Giải bài 6 trang 39 SGK Hình học lớp 12
Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều canh 2a. Tính diện tích xung quanh và thể tích của hình nón đó.
Đề bài
Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh \(2a\). Tính diện tích xung quanh và thể tích của hình nón đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Tính độ dài đường sinh \(l\) và bán kính đáy \(r\) của hình nón.
+) Tính độ dài đường cao của hình nón, sử dụng công thức \(h = \sqrt {{l^2} - {r^2}} \).
+) Tính diện tích xung quanh và thể tích của hình nón đó: \({S_{xq}} = \pi rl,\,\,V = \frac{1}{3}\pi {r^2}h\)
Lời giải chi tiết
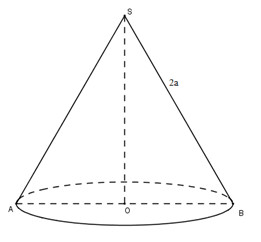
Theo đề bài, đường kính của hình tròn đáy của nón bằng \(\displaystyle 2a\).
Vậy bán kính \(\displaystyle r = a\) và độ dài đường sinh của hình nón \(\displaystyle l = 2a\).
Suy ra chiều cao của hình nón: \(\displaystyle h = \sqrt {{l^2} - {r^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
Vậy diện tích xung quanh của hình nón là: \(\displaystyle S_{xq} = πrl = π.a.2a=2a^2π\)
Thể tích khối nón là: \(\displaystyle V = {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {a^2}.a\sqrt 3 = {{\pi {a^3}\sqrt 3 } \over 3}\)
Loigiaihay.com
- Giải bài 7 trang 39 SGK Hình học lớp 12
- Giải bài 8 trang 40 SGK Hình học lớp 12
- Giải bài 9 trang 40 SGK Hình học lớp 12
- Giải bài 10 trang 40 SGK Hình học lớp 12
- Giải bài 5 trang 39 SGK Hình học lớp 12
>> Xem thêm



















