Giải bài 2 trang 49 SGK Hình học lớp 12
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Hãy xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.
Đề bài
Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng \(a\). Hãy xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.
Phương pháp giải - Xem chi tiết
+) Sử dụng đính lý Pi-ta-go để tính các cạnh và tìm tâm, tính bán kính của mặt cầu ngoại tiếp khối chóp.
Lời giải chi tiết
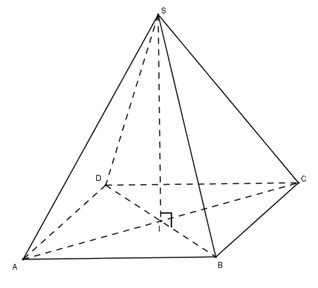
Gọi \(I = AC ∩ BD\).
Ta có ABCD là hình vuông cạnh \(a\) nên ta có: \(AC = BD = AB\sqrt 2 = a\sqrt 2 .\)
\(\Delta ASC\) có \(S{A^2} + S{C^2} = {a^2} + {a^2} = 2{a^2} = A{C^2}\) nên là tam giác vuông cân tại \(S\).
Tương tự tam giác SBD cũng vuông cân tại S.
\( \Rightarrow \dfrac{1}{{S{I^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{S{C^2}}}\) \( = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{2}{{{a^2}}} \Rightarrow SI = \dfrac{{a\sqrt 2 }}{2}.\)
\( \Rightarrow IA = IB = IC = ID = IS = \dfrac{{a\sqrt 2 }}{2}\)
Vậy mặt cầu ngoại tiếp hình chóp \(SABCD\) có tâm \(I\) và bán kính \(R= \dfrac{{a\sqrt 2 }}{2}.\)
Cách khác:
Có thể tính IS như sau:
\(IS = \sqrt {S{A^2} - A{I^2}} \) \( = \sqrt {{a^2} - \dfrac{{2{a^2}}}{4}} = \dfrac{{a\sqrt 2 }}{2}\)
Từ đó ta cũng kết luận được I là tâm mặt cầu ngoại tiếp hình chóp và bán kính bằng \(\dfrac{{a\sqrt 2 }}{2}\).
Loigiaihay.com
- Giải bài 3 trang 49 SGK Hình học lớp 12
- Giải bài 4 trang 49 SGK Hình học lớp 12
- Giải bài 5 trang 49 SGK Hình học lớp 12
- Giải bài 6 trang 49 SGK Hình học lớp 12
- Giải bài 7 trang 49 SGK Hình học lớp 12
>> Xem thêm



















