Có ba tổ dựng lều ở ba vị trí A, B, C như Hình 6. Ban tổ chức đặt ba thùng có dung tích bằng nhau tại một điểm tập kết chung. Mỗi tổ có sáu người, được phát một chiếc gàu giống nhau, các thành viên trong tổ chia thành từng cặp cõng nhau, múc nước từ tại của mình về đổ vào thùng tại điểm tập kết. Thùng của tổ nào đầy trước thì tổ đó chiến thắng. Để trò chơi công bằng, cần tìm điểm tập kết cách đều ba lều. Hãy xác định điểm đó.
Dựa vào đường tròn ngoại tiếp có tâm là giao điểm của ba đường trung trực của tam giác và có bán kính bằng khoảng cách từ giao điểm đó đến một đỉnh bất kì của tam giác.
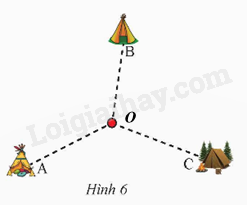
Điểm tập kết cách đều 3 lều tức khoảng cách từ điểm tập kết đều mỗi lều là như nhau tam giác. Điểm tập kết O là tâm đường tròn ngoại tiếp tam giác ABC.
Suy ra điểm tập kết O là giao điểm của ba đường trung trực của tam giác ABC. Khi vẽ, ta chỉ cần vẽ hai đường trung trực của tam giác ABC là ta có thể xác định được điểm O.

Các bài tập cùng chuyên đề
Cho tam giác ABC có \(AC = 3cm,AB = 4cm\) và \(BC = 5cm\). Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
Xác định tâm và bán kính của đường tròn ngoại tiếp mỗi tam giác sau:
a) Tam giác đều MNP có cạnh bằng 4cm;
b) Tam giác EFG có EF = 5 cm; EG = 3 cm; FG = 4cm.
Xác định tâm và bán kính đường tròn nội tiếp tam giác đều MNP có độ dài cạnh bằng 8 cm.
Xác định tâm và bán kính đường tròn ngoại tiếp hình chữ nhật ABCD trong mỗi trường hợp sau:
a) AB = 6 cm, BC = 8 cm;
b) AC = 9cm.
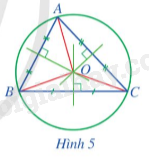
Cho tam giác ABC có O là giao điểm của ba đường trung trực (Hình 5).
a) Các đoạn thẳng OA, OB, OC có bằng nhau không?
b) Đặt R = OA. Đường tròn (O;R) có phải là đường tròn ngoại tiếp tam giác ABC hay không? Vì sao?
Tính bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A với AB = 5cm, AC = 12cm.
Tam giác đều ABC có cạnh bằng 4, M là trung điểm của BC và O là trọng tâm. Xác định tâm, bán kính và vẽ đường tròn ngoại tiếp tam giác ABC và AMC.
Tính bán kính đường tròn nội tiếp tam giác đều ABC có cạnh là \(2\sqrt 3 \)cm.
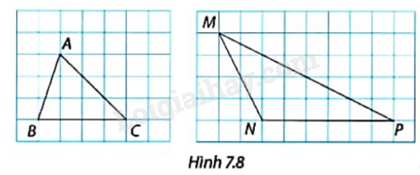
Vẽ các tam giác trong Hình 7.8 vào vở. Mỗi hình vuông trong lưới ô vuông đều có độ dài là 1. Hãy xác định tâm và vẽ đường tròn ngoại tiếp của mỗi tam giác.
Tâm đường tròn ngoại tiếp tam giác là giao của các đường
-
A.
trung trực.
-
B.
phân giác.
-
C.
trung tuyến.
-
D.
đường cao.
-
A.
Ba đường trung tuyến
-
B.
Ba đường trung trực
-
C.
Ba đường cao
-
D.
Ba đường phân giác
Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K. Tìm tâm đường tròn ngoại tiếp mỗi tam giác sau:
a) Tam giác BDE;
b) Tam giác DEC
c) Tam giác ADE.
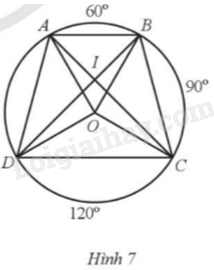
Trên đường tròn (O) bán kính R, lấy các điểm A, B, C, D sao cho \(sđ\overset\frown{AB}={{60}^{o}}\); \(sđ\overset\frown{BC}={{90}^{o}}\); \(sđ\overset\frown{CD}={{120}^{o}}\) (Hình 7).
a) Xác định tâm và tính theo R bán kính đường tròn ngoại tiếp của các tam giác OAB, OBC, OAD, OCD.
b) Gọi I là giao điểm của AC và BD. Tính bán kính đường tròn ngoại tiếp của các tam giác IAB, IBC, IAD, IDC.
Cho tam giác ABC có BC = 10 và \(\widehat {BAC} = {30^o}\). Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Cho tam giác ABC nội tiếp đường tròn (O) và ngoại tiếp đường tròn (I). Tia AI cắt (O) tại X (khác A). Chứng minh rằng X là tâm của đường tròn ngoại tiếp tam giác BIC.
Cho tam giác ABC có AB = AC = 12 cm và \(\widehat {BAC} = {120^o}\). Xác định tâm và tính bán kính của đường tròn (O; R) ngoại tiếp tam giác ABC.
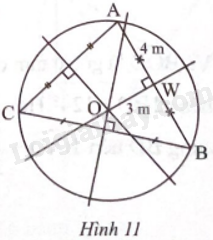
Để giữ vệ sinh trong một khu hội chợ, cứ mỗi cụm 3 quầy hàng A, B, C người ta đặt lại một thùng rác tại điểm O cách đều A, B, C. Cho biết có một nhà vệ sinh W nằm chính giữa hai quầy hàng A, B và khoảng cách từ W đến A và O lần lượt là 4 m và 3 m (Hình 11). Tính khoảng cách từ mỗi quầy hàng đến điểm đặt thùng rác.
Cho tam giác ABC có (O) là đường tròn ngoại tiếp. Vẽ đường cao AH của tam giác ABC và đường kính AD của đường tròn (O). Biết AB = 8 cm; AC = 15 cm và AH = 5 cm.
a) Chứng minh \(\Delta AHB\backsim \Delta ACD\).
b) Tính độ dài bán kính của đường tròn
Khẳng định nào dưới đây là đúng?
A. Tâm đường tròn ngoại tiếp một tam giác là giao điểm của ba đường phân giác.
B. Tâm đường tròn nội tiếp một tam giác là giao điểm của ba đường trung trực.
C. Tâm đường tròn nội tiếp một tam giác đều là trọng tâm của tam giác đó.
D. Tâm đường tròn ngoại tiếp một tam giác vuông là trọng tâm của tam giác đó.
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3cm. Tính diện tích tam giác ABC.
Trong một khu vui chơi có dạng hình tam giác đều có cạnh bằng 60m, người ta muốn tìm một vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng. Biết rằng bộ phát sóng đó có tầm phát sóng tối đa 50m, hỏi rằng có thể tìm được vị trí để đặt bộ phát sóng như vậy hay không?







Danh sách bình luận