Lý thuyết số phức
Số phức z = a + bi có phần thực là a, phần ảo là b
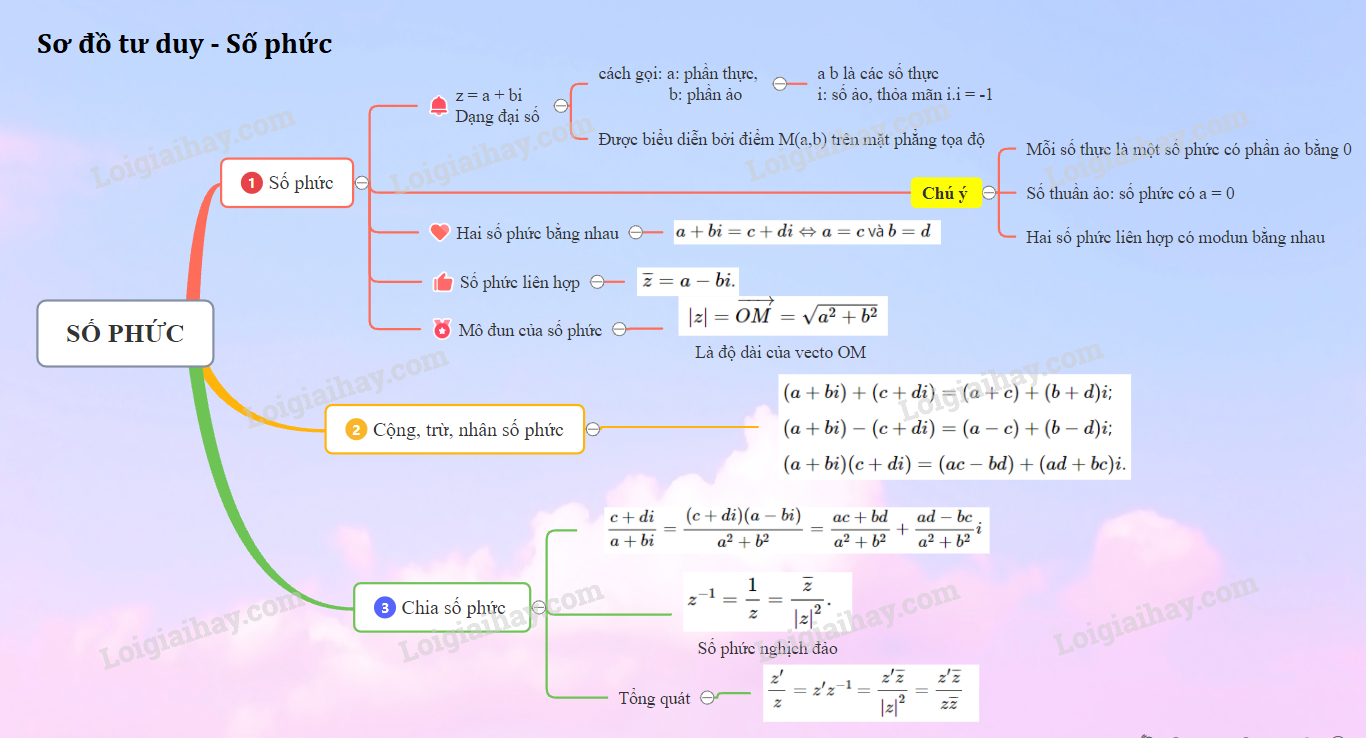
- Số phức \(z = a + bi\) có phần thực là \(a\), phần ảo là \(b\) (\(a, b \in \mathbb R\) và \(i^2 =-1\))
- Số phức bằng nhau \(a + bi = c + di ⇔ a = c\) và \(b = d\)
- Số phức \(z = a + bi\) được biểu diễn bởi điểm \(M(a;b)\) trên mặt phẳng toạ độ.
- Độ dài của \(\overrightarrow {OM} \) là môđun của số phức z, kí hiệu là \(|z| = \overrightarrow {OM} = \sqrt {{a^2} + {b^2}} \)
- Số phức liên hợp của \(z = a + bi\) và \( \overline z= a - bi\).
Chú ý
- Mỗi số thực là số phức có phần ảo bằng \(0\). Ta có \(\mathbb R ⊂ \mathbb C\).
- Số phức \(bi\) (\(b \in \mathbb R\)) là số thuần ảo (phần thực bằng \(0\))
- Số \(i\) được gọi là đơn vị ảo.
- Số phức viết dưới dạng \(z = a + bi\) (\(a, b \in R\)), gọi là dạng đại số của số phức.
- Ta có: \(|\overline z|= |z|\)
\( z = \overline z ⇔ z\) là số thực.
\(z = -\overline z ⇔ z\) là số ảo.
Loigiaihay.com
- Trả lời câu hỏi 1 trang 130 SGK Giải tích 12
- Trả lời câu hỏi 2 trang 131 SGK Giải tích 12
- Trả lời câu hỏi 3 trang 132 SGK Giải tích 12
- Trả lời câu hỏi 4 trang 132 SGK Giải tích 12
- Trả lời câu hỏi 5 trang 132 SGK Giải tích 12
>> Xem thêm



















