-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Bài 3. Khái niệm về thể tích của khối đa diện
Giải bài 4 trang 25 SGK Hình học 12
Cho hình chóp S.ABC. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A’, B’, C’ khác với S. Chứng minh rằng:
Đề bài
Cho hình chóp \(S.ABC\). Trên các đoạn thẳng \(SA, SB, SC\) lần lượt lấy ba điểm \(A’, B’, C’\) khác với \(S\). Chứng minh rằng
\(\displaystyle{{{V_{S.A'B'C'}}} \over {{V_{S.ABC}}}} = {{SA'} \over {SA}} \cdot {{SB'} \over {SB}} \cdot {{SC'} \over {SC}}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Gọi \(h\) và \(h'\) lần lượt là chiều cao hạ từ \(A\) và \(A'\) đến \((SBC)\), dựa vào định lí Vi-et tính tỉ số \(\frac{h'}{{h}}\).
+) Sử dụng công thức tính diện tích \({S_{\Delta SB'C'}} = \frac{1}{2}SB.SC.\sin \widehat {BSC}\) tính diện tích tam giác \(SB'C'\), tương tự tính diện tích tam giác \(SBC\), sau đó suy ra tỉ số \(\dfrac{{{S_{\Delta SB'C'}}}}{{{S_{\Delta SBC}}}}\).
+) Sử dụng công thức tính thể tích \(V = \dfrac{1}{3}S.h\) lập tỉ số thể tích \(S.A'B'C'\) và \(S.ABC\), rút gọn và suy ra kết quả.
Lời giải chi tiết
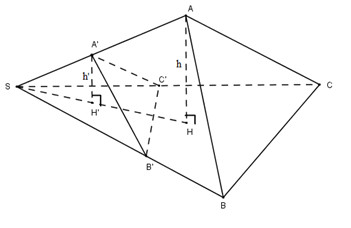
Gọi \(h\) và \(h’\) lần lượt là chiều cao hạ từ \(A, A’\) đến mặt phẳng \((SBC)\).
* Do \(A’H’// AH\) nên bốn điểm \(A, A’; H’\) và \(H\) đồng phẳng. (1)
Lại có, 3 điểm \(A, S, H\) đồng phẳng (2).
Từ (1) và (2) suy ra, 5 điểm \(A, A’, S. H\) và \(H’\) đồng phẳng.
Trong mp(ASH) ta có: \(\left\{ \begin{array}{l}A'H' \bot SH'\\AH \bot SH\\A'H'//AH\end{array} \right. \Rightarrow SH' \equiv SH\)
⇒ Ba điểm \(S, H\) và \(H’\) thẳng hàng.
Gọi \(S_1\) và \(S_2\) theo thứ tự là diện tích các tam giác \(SBC\) và \(SB’C’\).
Khi đó ta có \(\displaystyle{{h'} \over h} = {{SA'} \over {SA}}\) (định lý Ta - let) và:
\(\dfrac{{{S_2}}}{{{S_1}}}=\dfrac{{{S_{SB'C'}}}}{{{S_{SBC}}}} \) \(= \dfrac{{\dfrac{1}{2}SB'.SC'.\sin \widehat {BSC}}}{{\dfrac{1}{2}SB.SC.\sin \widehat {BSC}}} = \dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)
Suy ra \(\displaystyle{{{V_{S.A'B'C'}}} \over {{V_{S.ABC}}}} = {{{V_{A'.SB'C'}}} \over {{V_{A.SBC}}}} = {{{1 \over 3}h'{S_2}} \over {{1 \over 3}h{S_1}}}\) \(=\dfrac{{h'}}{h}.\dfrac{{{S_2}}}{{{S_1}}}\) \( = \displaystyle{{SA'} \over {SA}} \cdot {{SB'} \over {SB}} \cdot {{SC'} \over {SC}}\)
Đó là điều phải chứng minh.
Chú ý: Từ nay về sau chúng ta được sử dụng bài tập này như một kết quả và không cần chứng minh lại.
Loigiaihay.com
Bình luận
Chia sẻ
- Giải bài 5 trang 26 SGK Hình học lớp 12
- Giải bài 6 trang 26 SGK Hình học lớp 12
- Giải bài 3 trang 25 SGK Hình học 12
- Giải bài 2 trang 25 SGK Hình học 12
- Giải bài 1 trang 25 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
