 Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 Bài 3. Đường thẳng vuông góc với mặt phẳng
Bài 3. Đường thẳng vuông góc với mặt phẳng
Bài 4 trang 105 SGK Hình học 11
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc...
Đề bài
Cho tứ diện \(OABC\) có ba cạnh \(OA, OB, OC\) đôi một vuông góc. Gọi \(H\) là chân đường vuông góc hạ từ \(O\) tới mặt phẳng \((ABC)\). Chứng minh rằng:
a) H là trực tâm của tam giác \(ABC\);
b) \(\dfrac{1}{OH^{2}}=\dfrac{1}{OA^{2}}+\dfrac{1}{OB^{2}}+\dfrac{1}{OC^{2}}.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh \(AB \bot CH;\,\,BC \bot AH\).
b) Sử dụng hệ thức lượng trong tam giác vuông.
Lời giải chi tiết
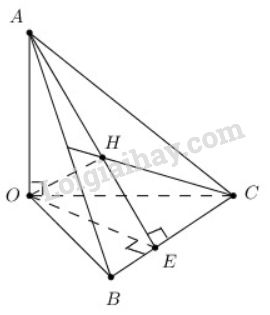
a) \(H\) là hình chiếu của \(O\) trên mp \((ABC)\) nên \(OH ⊥ (ABC) \Rightarrow OH ⊥ BC\).
Mặt khác: \(OA ⊥ OB\), \(OA ⊥ OC\)
\(\Rightarrow OA ⊥ (OBC) \Rightarrow OA ⊥ BC\)
\(\left\{ \begin{array}{l}
BC \bot OH\\
BC \bot OA\\
OA \cap OH = O
\end{array} \right.\) \( \Rightarrow BC \bot \left( {OAH} \right)\)
Mà \(AH \subset \left( {OAH} \right)\) \(\Rightarrow BC ⊥ AH\) (1)
Ta có: \(\left\{ \begin{array}{l}OB \bot OA\\OB \bot OC\end{array} \right. \Rightarrow OB \bot \left( {OAC} \right)\)
Mà \(AC \subset \left( {OAC} \right) \Rightarrow OB \bot AC\)
\(OH \bot \left( {ABC} \right) \Rightarrow OH \bot AC\)
Do đó \(\left\{ \begin{array}{l}OB \bot AC\\OH \bot AC\end{array} \right. \Rightarrow AC \bot \left( {OBH} \right)\) \( \Rightarrow AC \bot BH\) (2)
Từ (1) và (2) ta có tam giác \(ABC\) có
\(\left\{ \begin{array}{l}
AH \bot BC\\
BH \bot AC\\
AH \cap BH = H
\end{array} \right.\)
\(\Rightarrow H\) là trực tâm của tam giác \(ABC\).
b) Trong mặt phẳng \((ABC)\) gọi \(E = AH ∩ BC\)
\(\left\{ \begin{array}{l}
OH \bot \left( {ABC} \right)\\
AE \subset \left( {ABC} \right)
\end{array} \right. \Rightarrow OH \bot AE\)
Ta có: \(\left\{ \begin{array}{l}OA \bot \left( {OBC} \right)\\OE \subset \left( {OBC} \right)\end{array} \right. \Rightarrow OA \bot OE\) \( \Rightarrow \Delta OAE\) vuông tại \(O\) có đường cao \(OH\)
\( \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{E^2}}}\) (hệ thức giữa cạnh và đường cao trong tam giác vuông \(OAE\))
Lại có: \(\left\{ \begin{array}{l}BC \bot \left( {OAH} \right)\\OE \subset \left( {OAH} \right)\end{array} \right. \Rightarrow BC \bot OE\)
Mà \(OB \bot OC\) nên \(\Delta OBC\) vuông tại \(O\) có \(OE\) là đường cao.
\( \Rightarrow \dfrac{1}{{O{E^2}}} = \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\)
Vậy \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{E^2}}}\)\( = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\) (đpcm).
Nhận xét: Biểu thức này là mở rộng của công thức tính đường cao thuộc cạnh huyền của tam giác vuông: \(\dfrac{1}{h^{2}}=\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}} .\)
Loigiaihay.com
- Bài 5 trang 105 SGK Hình học 11
- Bài 6 trang 105 SGK Hình học 11
- Bài 7 trang 105 SGK Hình học 11
- Bài 8 trang 105 SGK Hình học 11
- Bài 3 trang 104 SGK Hình học 11
>> Xem thêm



















