Bài 9 trang 71 SGK Toán 8 tập 1
Tứ giác ABCD có AB= BC và AC tia phân giác cưa góc A. Chứng minh rằng ABCD là hình thang.
Đề bài
Tứ giác \(ABCD\) có \(AB= BC\) và \(AC\) tia phân giác của góc \(A\). Chứng minh rằng \(ABCD\) là hình thang.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Dấu hiệu nhận biết hình thang: Hình thang là tứ giác có hai cạnh đối song song.
- Chứng minh hai đường thẳng song song ta chứng minh cặp góc so le trong bằng nhau.
Lời giải chi tiết
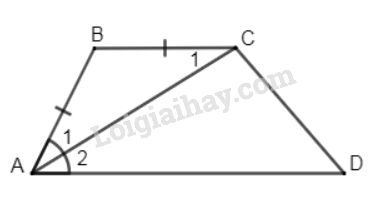
Ta có \(AB = BC\) (giả thiết)
Suy ra \(∆ABC\) cân tại \(B\) (định nghĩa tam giác cân)
Nên \(\widehat{A_{1}}=\widehat{C_{1}}\) (1) (tính chất tam giác cân)
Lại có, \(AC\) là tia phân giác của \(\widehat{A}\) (giả thiết) nên suy ra \(\widehat{A_{1}}= \widehat{A_{2}}\) (2) (tính chất tia phân giác )
Từ (1) và (2) suy ra \(\widehat{C_{1}}=\widehat{A_{2}}\) mà hai góc này ở vị trí so le trong nên \(BC // AD\) (Dấu hiệu nhận biết hai đường thẳng song song)
Vậy tứ giác \(ABCD\) là hình thang.
- Bài 10 trang 71 SGK Toán 8 tập 1
- Đề kiểm tra 15 phút - Đề số 1 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 1 - Hình học 8
>> Xem thêm


















