-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Câu hỏi tự luyện Toán 11
-
TẢI 50 ĐỀ KIỂM TRA 15 PHÚT TOÁN 11
-
TẢI 30 ĐỀ KIỂM TRA 1 TIẾT TOÁN 11
-
TẢI 5 ĐỀ THI GIỮA KÌ 1 TOÁN 11
-
TẢI 25 ĐỀ THI HỌC KÌ 1 TOÁN 11
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 11
-
TẢI 20 ĐỀ THI HỌC KÌ 2 TOÁN 11
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Ôn tập chương III - Vectơ trong không gian. Quan hệ vuô..
Bài 11 trang 125 SGK Hình học 11
Khoảng cách giữa hai cạnh đối của một tứ diện đều cạnh a là bằng:
Đề bài
Khoảng cách giữa hai cạnh đối của một tứ diện đều cạnh \(a\) là bằng:
(A) \({{3a} \over 2}\) (B) \({{a\sqrt 2 } \over 2}\)
(C) \({{a\sqrt 3 } \over 2}\) (D) \(a\sqrt2\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Xác định đoạn vuông góc chung của hai đường thẳng \(AB\) và \(CD\). Tính độ dài đoạn vuông góc chung đó.
(Đoạn nối hai trung điểm hai cạnh đối diện của một tứ diện đều là đoạn vuông góc chung của hai cạnh đó)
Lời giải chi tiết
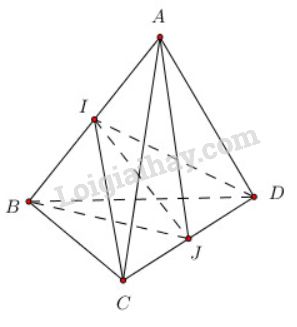
Gọi \(I\) là trung điểm cạnh \(AB\); \(J\) là trung điểm của cạnh \(CD\).
Ta có: \(\Delta ACD = \Delta BCD\,\,\left( {c.c.c} \right) \Rightarrow AJ = BJ\) (hai đường trung tuyến tương ứng).
\( \Rightarrow \Delta JAB\) cân tại J \( \Rightarrow JI \bot AB\).
Chứng minh tương tự \(\Delta ICD\) cân tại I \(\Rightarrow IJ \bot CD\).
\(\Rightarrow IJ\) là đoạn vuông góc của cạnh \(AB\) và \(CD\).
\( \Rightarrow d\left( {AB;CD} \right) = IJ\)
Tứ diện cạnh a nên:
\(\eqalign{
& BJ = {{a\sqrt 3 } \over 2},BI = {a \over 2} \cr
& \Rightarrow {\rm{I}}{{\rm{J}}^2} = B{J^2} - B{I^2} \cr
& \Rightarrow {\rm{I}}{{\rm{J}}^2} = {{2{a^2}} \over 4} \Rightarrow {\rm{I}}{{\rm{J}}^2} = {{a\sqrt 2 } \over 2} \cr} \)
Vậy \(d\left( {AB;CD} \right) = \frac{{a\sqrt 2 }}{2}\).
Loigiaihay.com
Bình luận
Chia sẻ- Bài 10 trang 124 SGK Hình học 11
- Bài 9 trang 124 SGK Hình học 11
- Bài 8 trang 124 SGK Hình học 11
- Bài 7 trang 124 SGK Hình học 11
- Bài 6 trang 123 SGK Hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
