Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Ôn tập chương III - Vectơ trong không gian. Quan hệ vuô..

Bài 6 trang 123 SGK Hình học 11


Tìm mệnh đề sai trong các mệnh đề sau đây:

Đề bài

Tìm mệnh đề sai trong các mệnh đề sau đây:

(A) Cho hai đường thẳng \(a\) và \(b\) trong không gian có các vecto chỉ phương lần lượt là \(\overrightarrow u ,\overrightarrow v \) . Điều kiện cần và đủ để \(a\) và \(b\) chéo nhau là \(a\) và \(b\) không có điểm chung và hai vecto \(\overrightarrow u ,\overrightarrow v \) không cùng phương.

(B) Gọi \(a\) và \(b\) là hai đường thẳng chéo nhau và vuông góc với nhau. Đường thẳng vuông góc chung của \(a\) và \(b\) nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.

(C) Không thể có một hình chóp tứ giác \(S.ABCD\) nào có hai mặt bên \((SAB)\) và \((SCD)\) cùng vuông góc với mặt phẳng đáy.

(D) Gọi \({\overrightarrow u ,\overrightarrow v } \) là cặp vecto chỉ phương của hai đường thẳng cắt nhau nằm trong mặt phẳng \((α)\) và \(\overrightarrow n \) là vecto chỉ phương của đường thẳng \(Δ\). Điều kiện cần và đủ để \(Δ ⊥ (α)\) là: \(\left\{ \matrix{\overrightarrow {n.} \overrightarrow u = 0 \hfill \cr \overrightarrow {n.} \overrightarrow v = 0 \hfill \cr} \right.\)

Video hướng dẫn giải

Lời giải chi tiết

(A) Từ giả thiết \(a\) và \(b\) không có điểm chung và các vecto \(\overrightarrow u ,\overrightarrow v \) của chúng không cùng phương, ta suy ra hai đường thẳng \(a, b\) không đồng phẳng vì chúng không trùng nhau, không cắt nhau, không song song với nhau. Vậy \(a\) và \(b\) chéo nhau. Ngược lại nếu \(a\) và \(b\) chéo nhau thì rõ ràng \(a\) và \(b\) không có điểm chung và \(\overrightarrow u ,\overrightarrow v \) không cùng phương.

Mệnh đề (A) đúng.

(B) \(a\) và \(b\) có đường vuông góc chung là \(c\), \(a ⊥ b\).

Ta có: \(\left. \matrix{a \bot b \hfill \cr a \bot c \hfill \cr} \right\} \Rightarrow a \bot (b,c)\)

Tương tự ta có: \(b ⊥ (a, c)\)

Mệnh đề (B) đúng.

(C) Xét trường hợp \(AB\) và \(CD\) cắt nhau tại một điểm \(H\).

Ta lấy \(S\) trên đường thẳng vuông góc với \(mp(ABCD)\) kẻ từ \(H\) thì rõ ràng \((SAB) ⊥(ABCD)\) và \((SCD) ⊥(ABCD)\)

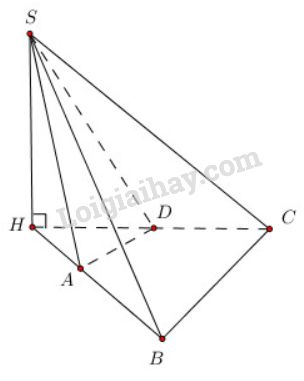
Vậy (C) sai.

(D) Đúng. \(\left\{ \begin{array}{l}\overrightarrow n .\overrightarrow u = 0\\\overrightarrow n .\overrightarrow v = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow n \bot \overrightarrow u \\\overrightarrow n \bot \overrightarrow v \end{array} \right. \Rightarrow \Delta \bot \left( \alpha \right)\)

Chọn đáp án C.

 Loigiaihay.com


Bình chọn:
4.3 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store