Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Bài 3. Phương trình và hệ phương trình bậc nhất nhiều ẩn
Bài 5 trang 68 SGK Đại số 10
Giải các hệ phương trình
Video hướng dẫn giải
Giải các hệ phương trình
LG a
\(\left\{\begin{matrix} x + 3y + 2z =8 & \\ 2x + 2y + z =6& \\ 3x +y+z=6;& \end{matrix}\right.\)
Phương pháp giải:
Giải hệ phương trình bằng phương pháp thế hoặc đưa về dạng tam giác để giải.
Lời giải chi tiết:
Phương pháp thế:
\(x + 3y + 2z = 8 \Rightarrow x = 8 - 3y - 2z\).
Thế vào phương trình thứ hai và thứ ba thì được
\( \Leftrightarrow \left\{\begin{matrix} x= 8 - 3y -2z & \\ 2(8-3y-2z)+2y +z=6& \\ 3(8-3y-2z) +y+z=6& \end{matrix}\right.\\ \Leftrightarrow \left\{\begin{matrix} x= 8 - 3y -2z & \\ 4y +3z=10& \\ 8y + 5z =18& \end{matrix}\right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x = 8 - 3y - 2z\\8y + 6z = 20\\8y + 5z = 18\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 8 - 3y - 2z\\z = 2\\8y + 5.2 = 18\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x = 8 - 3y - 2z\\z = 2\\y = 1\end{array} \right.\end{array}\)
\(\Leftrightarrow \left\{ \begin{array}{l}
x = 1\\
y = 1\\
z = 2
\end{array} \right.\)
Nghiệm của hệ phương trình ban đầu là \((1; 1; 2)\).
Chú ý:
Ta có thể đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số như sau:
Nhân cả hai phương trình dưới với 2 rồi trừ cho phương trình đầu ta được:
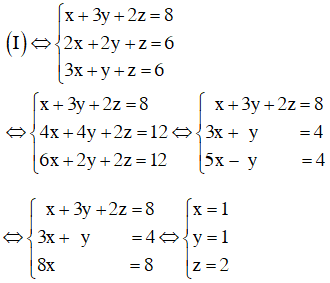
LG b
\(\left\{\begin{matrix} x - 3y + 2z =-7 & \\ -2x + 4y + 3z =8& \\ 3x +y-z=5.& \end{matrix}\right.\)
Phương pháp giải:
Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.
Lời giải chi tiết:
Rút x từ phương trình đầu tiên sau đó thay vào các phương trình còn lại của hệ.
\(\begin{array}{l}
\left\{ \begin{array}{l}
x = - 7 + 3y - 2z\\
- 2\left( { - 7 + 3y - 2z} \right) + 4y + 3z = 8\\
3\left( { - 7 + 3y - 2z} \right) + y - z = 5
\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}
x = - 7 + 3y - 2z\\
14 - 6y + 4z + 4y + 3z = 8\\
- 21 + 9y - 6z + y - z = 5
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = - 7 + 3y - 2z\\
- 2y + 7z = - 6\\
10y - 7z = 26
\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}
x = - 7 + 3y - 2z\\
8y = 20\\
10y - 7z = 26
\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}
x = - 7 + 3y - 2z\\
y = \frac{5}{2}\\
z = - \frac{1}{7}
\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{{11}}{{14}}\\
y = \frac{5}{2}\\
z = - \frac{1}{7}
\end{array} \right.
\end{array}\)
Cách khác:
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (1) với 3 rồi trừ đi phương trình (3) ta được:
\(\left\{ \begin{array}{l}
x - 3y + 2z = - 7\\
- 2y + 7z = - 6\\
- 10y + 7z = - 26
\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}
x - 3y + 2z = - 7\\
- 2y + 7z = - 6\\
8y = 20
\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
x - 3.\frac{5}{2} + 2z = - 7\\
- 2.\frac{5}{2} + 7z = - 6\\
y = \frac{5}{2}
\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}
x + 2z = \frac{{1}}{2}\\
7z = - 1\\
y = \frac{5}{2}
\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}
x + 2.\left( { - \frac{1}{7}} \right) = \frac{{1}}{2}\\
z = - \frac{1}{7}\\
y = \frac{5}{2}
\end{array} \right. \) \( \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{11}{14}\\
y = \frac{5}{2}\\
z = - \frac{1}{7}
\end{array} \right.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 6 trang 68 SGK Đại số 10
- Bài 7 trang 68 SGK Đại số 10
- Hệ phương trình có cấu trúc đặc biệt
- Bài 4 trang 68 SGK Đại số 10
- Bài 3 trang 68 SGK Đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
