 Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
 Bài 3. Phương trình và hệ phương trình bậc nhất nhiều ẩn
Bài 3. Phương trình và hệ phương trình bậc nhất nhiều ẩn
Bài 2 trang 68 SGK Đại số 10
Giải các hệ phương trình
Video hướng dẫn giải
Giải các hệ phương trình
LG a
\(\left\{\begin{matrix} 2x - 3y = 1 & \\ x + 2y = 3;& \end{matrix}\right.\)
Phương pháp giải:
Ta có thể giải hệ phương trình bằng phương pháp thế, hoặc phương pháp cộng đại số.
Lời giải chi tiết:
Giải bằng phương pháp thế:
\(\left\{ \begin{array}{l}
2x - 3y = 1\,\,\left( 1 \right)\\
x + 2y = 3\,\,\left( 2 \right)
\end{array} \right.\)
Từ (2) suy ra x = 3 – 2y, thế vào phương trình (1) ta được:
2.(3 – 2y) – 3y = 1
⇔ 6 – 4y – 3y = 1
⇔ 7y = 5
⇔ y = 5/7.
Thay y = 5/7 vào x = 3 – 2y ta được :
x = 3 – 2.5/7 = 11/7.
Vậy hệ phương trình có nghiệm (x ; y) = (11/7 ; 5/7).
Kết luận: Hệ phương trình có nghiệm duy nhất (\(\dfrac{11}{7}\); \(\dfrac{5}{7}\)).
Giải bằng phương pháp cộng đại số:
\(\left\{ \begin{array}{l}
2x - 3y = 1\\
x + 2y = 3
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
2x - 3y = 1\\
- 2x - 4y = - 6
\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}
- 7y = - 5\\
2x - 3y = 1
\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
y = \frac{5}{7}\\
2x - 3.\frac{5}{7} = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = \frac{5}{7}\\
2x = \frac{{22}}{7}
\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
y = \dfrac{5}{7}\\
x = \dfrac{{11}}{7}
\end{array} \right.\)
LG b
\(\left\{\begin{matrix} 3x + 4y = 5 & \\ 4x - 2y = 2;& \end{matrix}\right.\)
Lời giải chi tiết:
\(\left\{ \begin{array}{l}
3x + 4y = 5\\
4x - 2y = 2
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
3x + 4y = 5\\
8x - 4y = 4
\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}
11x = 9\\
3x + 4y = 5
\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{9}{{11}}\\
3.\frac{9}{{11}} + 4y = 5
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{9}{{11}}\\
4y = \frac{{28}}{{11}}
\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
x = \dfrac{9}{{11}}\\
y = \dfrac{7}{{11}}
\end{array} \right.\)
Đáp số: (\(\dfrac{9}{11}\); \(\dfrac{7}{11}\)).
Cách khác:
\(\left\{\begin{matrix} 3x + 4y = 5 \,\,(1)& \\ 4x - 2y = 2\,\,(2)& \end{matrix}\right.\)
Ta có: \(\left( 2 \right) \Leftrightarrow 2x - y = 1 \Leftrightarrow y = 2x - 1\)
Thế y=2x-1 vào phương trình (1) ta được
3x + 4.(2x – 1) = 5
⇔ 3x + 8x – 4 = 5
⇔ 11x = 9
⇔ x = 9/11
Thay vào phương trình y = 2x – 1 ta được y = 2.9/11 – 1 = 7/11.
Vậy hệ phương trình có nghiệm (x; y) = (9/11; 7/11)
LG c
\(\left\{\begin{matrix} \dfrac{2}{3}x +\dfrac{1}{2}y =\dfrac{2}{3}& \\ \dfrac{1}{3}x - \dfrac{3}{4}y= \dfrac{1}{2}& \end{matrix}\right.\)
Lời giải chi tiết:
Hệ đã cho \( \Leftrightarrow \) \(\left\{\begin{matrix} 4x + 3y = 4 & \\ 4x - 9y = 6& \end{matrix}\right.\)
(Nhân cả hai vế của pt trên với 6, nhân cả hai vế của pt dưới với 12)
\(\Leftrightarrow \left\{\begin{matrix} 4x + 3y = 4 & \\ 12y =-2\end{matrix}\right.\)
(Lấy phương trình thứ nhất trừ đi phương trình thứ hai)
\( \Leftrightarrow \left\{ \begin{array}{l}
4x + 3.\left( { - \frac{1}{6}} \right) = 4\\
y = - \frac{1}{6}
\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}
4x = \frac{9}{2}\\
y = - \frac{1}{6}
\end{array} \right.\)
\( \Leftrightarrow \) \(\left\{\begin{matrix} x = \dfrac{9}{8} & \\ y =-\dfrac{1}{6}\end{matrix}\right.\).
Cách khác:
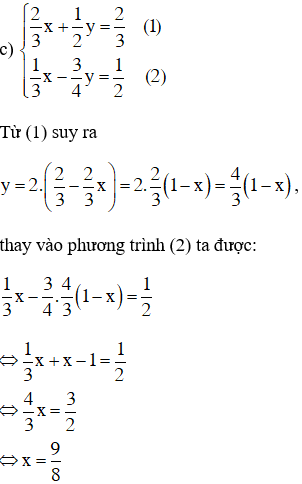
Thay \(x = \frac{9}{8}\) vào \(y = \frac{4}{3}\left( {1 - x} \right) = \frac{4}{3}\left( {1 - \frac{9}{8}} \right) = - \frac{1}{6}\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\frac{9}{8}; - \frac{1}{6}} \right)\).
LG d
\(\left\{\begin{matrix} 0,3x - 0,2y =0,5 & \\ 0,5x + 0,4y = 1,2.& \end{matrix}\right.\)
Lời giải chi tiết:
Hệ \( \Leftrightarrow \left\{\begin{matrix} 3x - 2y = 5 & \\ 5x + 4y = 12\end{matrix}\right.\)
(Nhân mỗi phương trình với \(10\))
\( \Leftrightarrow \left\{ \begin{array}{l}
6x - 4y = 10\\
5x + 4y = 12
\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}
11x = 22\\
5x + 4y = 12
\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
5.2 + 4y = 12
\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
4y = 2
\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
y = \frac{1}{2}
\end{array} \right.\)
Cách 2:
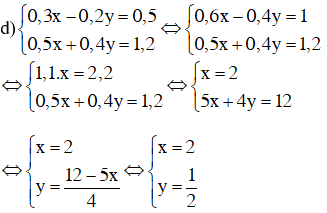
Cách 3:
Hệ \( \Leftrightarrow \left\{\begin{matrix} 3x - 2y = 5 \,\,(1)& \\ 5x + 4y = 12\,\,(2)\end{matrix}\right.\)
Từ (1) rút ra 2y = 3x – 5, thay vào phương trình (2) ta được:
5x + 2.(3x – 5) = 12
⇔ 5x + 6x – 10 = 12
⇔ 11x = 22
⇔ x = 2.
Thay x = 2 vào phương trình 2y = 3x – 5 ta được 2y = 1 ⇔ y = 1/2.
Vậy hệ phương trình có nghiệm (x ; y) = (2 ; 1/2)
Loigiaihay.com
- Bài 3 trang 68 SGK Đại số 10
- Bài 4 trang 68 SGK Đại số 10
- Bài 5 trang 68 SGK Đại số 10
- Bài 6 trang 68 SGK Đại số 10
- Bài 7 trang 68 SGK Đại số 10
>> Xem thêm



















