Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Ôn tập cuối năm - Đại số - Toán 8

Bài 5 trang 130 SGK Toán 8 tập 2


Đề bài

Chứng minh rằng:

\(\dfrac{{{a^2}}}{{a + b}} + \dfrac{{{b^2}}}{{b + c}} + \dfrac{{{c^2}}}{{c + a}} = \dfrac{{{b^2}}}{{a + b}} \)\(\,+ \dfrac{{{c^2}}}{{b + c}} + \dfrac{{{a^2}}}{{c + a}}\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Ta chứng minh hiệu hai vế bằng \(0\).

Sử dụng hằng đẳng thức số 3: \({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\)

Lời giải chi tiết

Xét hiệu hai vế: 

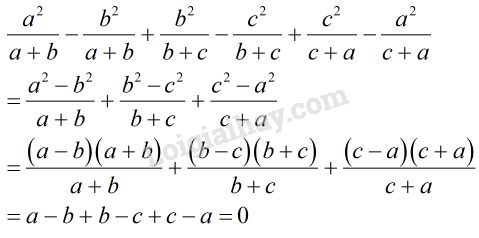
\(\Rightarrow\) \(\dfrac{{{a^2}}}{{a + b}} + \dfrac{{{b^2}}}{{b + c}} + \dfrac{{{c^2}}}{{c + a}} = \dfrac{{{b^2}}}{{a + b}} \)\(\,+ \dfrac{{{c^2}}}{{b + c}} + \dfrac{{{a^2}}}{{c + a}}\) 

Loigiaihay.com


Bình chọn:
4.4 trên 40 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 8 trên Tuyensinh247.com cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua