Bài 34 trang 119 SGK Toán 9 tập 1

Cho hai đường tròn (O; 20cm) và (O'; 15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO', biết rằng AB=24cm.

Đề bài

Cho hai đường tròn $(O;\ 20cm)$ và $(O'; 15cm)$ cắt nhau tại $A$ và $B$ . Tính đoạn nối tâm $OO'$ , biết rằng $AB=24cm.$ (Xét hai trường hợp: $O$ và $O'$ nằm khác phía đối với $AB;\ O$ và $O'$ nằm cùng phía đối với $AB$ ).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Nếu $(O)$ và $(O')$ cắt nhau tại $A,\ B$ thì $OO'$ là trung trực của $AB$ .

+) Định lí Pytago: $\Delta{ABC}$ vuông tại $A$ thì $BC^2=AB^2+AC^2$ .

Lời giải chi tiết

* TH1: $O$ và $O'$ nằm khác phía đối với $AB$ (h.a)

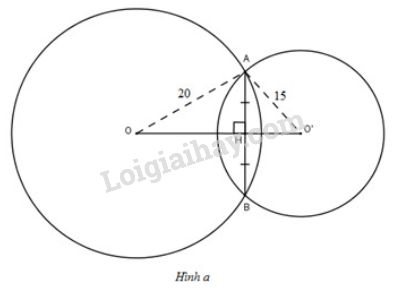
Vẽ dây cung $AB$ cắt $OO'$ tại $H$ . Theo định lí - trang 119 về tính chất đường nối tâm, ta có: $AB\perp OO'$ và $HA=HB=\dfrac{24}{2}=12cm$ .

Xét tam giác $AOH$ vuông tại $H$ , áp dụng định lí Pytago, ta có:

$OA^2=OH^2+AH^2$

$\Rightarrow OH^2=OA^2-AH^2=20^{2}-12^{2}=256$

$\Leftrightarrow OH=\sqrt{256}=16cm.$

Xét tam giác $AO'H$ vuông tại $H$ , áp dụng định lí Pytago, ta có:

$AO'^2=AH^2+HO'^2$

$\Rightarrow HO'^2=AO'^2 - AH^2=15^2-12^2=81$

$\Leftrightarrow HO'=\sqrt {81}=9(cm)$ .

Khi đó $OO'=OH+HO'=16+9=25(cm).$

*TH2: $O$ và $O'$ nằm cùng phía đối với $AB$ (h.b)

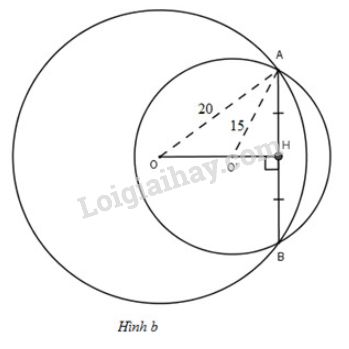
Tương tự TH1 ta vẫn có $OH=16cm;O'H=9cm$

Khi đó $OO'=OH-O'H=16-9=7(cm).$

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 75 phiếu

Bài tiếp theo

Bài 33 trang 119 SGK Toán 9 tập 1
Trên hình 89 hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC//O'D.
Trả lời câu hỏi Bài 7 trang 119 Toán 9 Tập 1
Cho hình 88.
Trả lời câu hỏi Bài 7 trang 118 SGK Toán 9 Tập 1
a) Quan sát hình 85, chứng minh rằng OO’ là đường trung trực của AB.
Trả lời câu hỏi Bài 7 trang 117 Toán 9 Tập 1
Giải Trả lời câu hỏi Bài 7 trang 117 Toán 9 Tập 1 . Ta gọi hai đường tròn không trùng nhau là hai đường tròn phân biệt.
Lý thuyết về vị trí tương đối của hai đường tròn
Vị trí tương đối của hai đường tròn

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com

>> Chi tiết khoá học xem: TẠI ĐÂY

Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.