Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 6. Tính chất của hai tiếp tuyến cắt nhau

Bài 31 trang 116 SGK Toán 9 tập 1


Tam giác ABC ngoại tiếp đường tròn (O).

Đề bài

Trên hình \(82\), tam giác \(ABC\) ngoại tiếp đường tròn \((O)\).

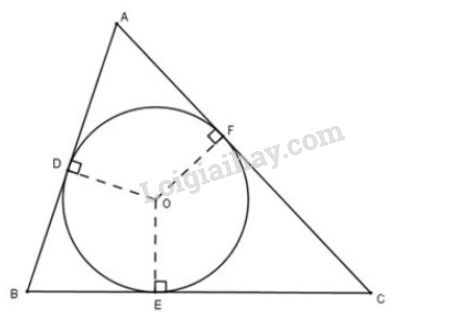
a) Chứng minh rằng:

\(2AD=AB+AC-BC.\)

b) Tìm các hệ thức tương tự hệ thức ở câu a).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Sử dụng tính chất hai tiếp tuyến cắt nhau để chứng minh các đoạn thẳng bằng nhau: Nếu \(AB,\ AC\) là hai tiếp tuyến của \((O)\) lần lượt tại \(A,\ B\) thì ta có: \(AB=AC\)

+) Chu vi tam giác \(ABC\) là \(C_{\Delta{ABC}}=AB+AC+BC\)

Lời giải chi tiết

a) Tam giác \(ABC\) ngoại tiếp đường tròn tâm \(O\) nên \(AB,\ BC,\ AC\) lần lượt là tiếp tuyến tại \(D,\ E,\ F\) của đường tròn.

Theo tính chất của hai tiếp tuyến cắt nhau ta có: 

\(AD=AF;\ DB=BE;\ FC=CE.\)

Xét vế phải:

\(VP=AB+AC-BC\)

\(=(AD+DB)+(AF+FC)-(BE+EC)\)

Thay \(DB=BE,\ FC=CE\) vào biểu thức trên, ta được:

\(VP=(AD+BE)+(AF+CE)-(BE+EC)\)

\(=AD+BE+AF+CE-BE-EC\)

\(=AD+AF+(BE-BE)+(CE-EC)\)

\(= AD+AF=2AD=VT.\) (Do \(AD=AF)\)

Vậy \(2AD=AB+AC-BC.\)

b) Các hệ thức tương tự là:

\(2BD=BA+BC-AC;\)

\(2CF=CA+CB-AB.\)

Nhận xét. 

Đặt \(p=\dfrac{AB+AC+BC}{2}\) là nửa chu vi của tam giác \(ABC\), \(AB=c;\ BC=a;\ CA=b\).

Ta có: \(2AD=AB+AC-BC\)

\(=(AB+AC+BC)-2BC\)

\(\Leftrightarrow AD=\dfrac{AB+AC+BC}{2}-\dfrac{2BC}{2}\)

\(\Leftrightarrow AD=p-BC\) hay \(AD=p-a\).

Tương tự ta có các kết quả sau:

\(AD=AF=p-a;\)

\(BD=BE=p-b;\)

\(CE=CF=p-c.\)

Loigiaihay.com


Bình chọn:
4.8 trên 46 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store