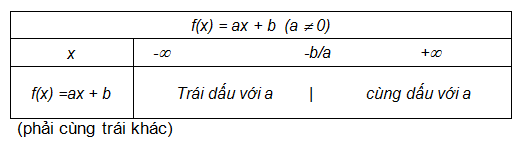Bài 1 trang 94 SGK Đại số 10
Xét dấu các biểu thức:...
Video hướng dẫn giải
Xét dấu các biểu thức:
LG a
\(f(x) = (2x - 1)(x + 3)\);
Phương pháp giải:
Cách lập bảng xét dấu:
- Biến đổi biểu thức đã cho về dạng tích (hoặc thương) các nhị thức bậc nhất
- Tìm các nhị thức bậc nhất có trong biểu thức.
- Tìm nghiệm của các nhị thức bậc nhất này.
- Sắp xếp các nghiệm theo thứ tự tăng dần.
- Lập bảng và xét dấu các nhị thức bậc nhất đó.
Bảng xét dấu của nhị thức bậc nhất được thể hiện qua bảng sau:
Lời giải chi tiết:
Ta có: \(2x - 1 = 0 \Leftrightarrow x = \dfrac{1}{2}\); \(x + 3 = 0 \Leftrightarrow x = - 3\)
Ta lập bảng xét dấu
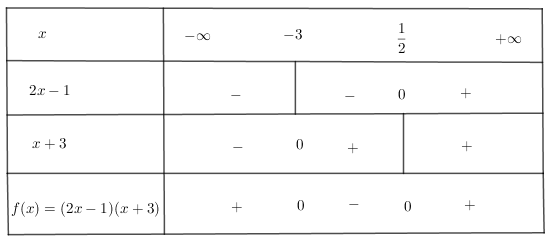
Kết luận:
+) \(f(x) < 0\) nếu \(- 3 < x < \dfrac{1}{2}\)
+) \(f(x) = 0\) nếu \(x = - 3\) hoặc \(x = \dfrac{1}{2}\)
+) \(f(x) > 0\) nếu \(x < - 3\) hoặc \(x > \dfrac{1}{2}\).
LG b
\(f(x) = (- 3x - 3)(x + 2)(x + 3)\);
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}
- 3x - 3 = 0 \Leftrightarrow x = - 1\\
x + 2 = 0 \Leftrightarrow x = - 2\\
x + 3 = 0 \Leftrightarrow x = - 3\\
\left( { - 3 < - 2 < - 1} \right)
\end{array}\)
Ta có bảng xét dấu

Vậy,
+) \( f(x) < 0\) nếu \(x ∈ (- 3; - 2) ∪ (- 1; +∞)\)
+) \(f(x) = 0\) với \(x = - 3\), \(x= - 2\), hoặc \(x= - 1\)
+) \( f(x) > 0\) với \(x ∈ (-∞; - 3) ∪ (- 2; - 1)\).
LG c
\( f(x) = \dfrac{-4}{3x+1}-\dfrac{3}{2-x};\)
Lời giải chi tiết:
TXĐ: \(\mathbb R \backslash \left\{ { - \frac{1}{3};2} \right\}\)
Ta có: \(f(x) = \dfrac{-4}{3x+1}-\dfrac{3}{2-x}\) \(= \dfrac{{ - 4\left( {2 - x} \right) - 3\left( {3x + 1} \right)}}{{\left( {3x + 1} \right)\left( {2 - x} \right)}} \) \(= \dfrac{{ - 8 + 4x - 9x - 3}}{{\left( {3x + 1} \right)\left( {2 - x} \right)}}\) \(=\dfrac{-5x-11}{(3x+1)(2-x)}\)
Lại có:
\(\begin{array}{l}
-5x - 11 = 0 \Leftrightarrow x = - \dfrac{{11}}{5}\\
3x + 1 = 0 \Leftrightarrow x = - \dfrac{1}{3}\\
2 -x= 0 \Leftrightarrow x = 2
\end{array}\)
Ta lập bảng xét dấu
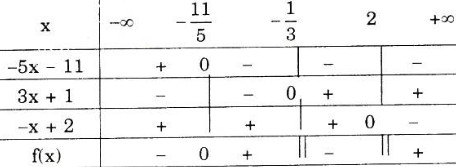
Vậy,
+) \(f(x)\) không xác định nếu \(x = -\dfrac{1}{3}\) hoặc \(x = 2\)
+) \(f(x) < 0\) với \(x ∈ \left ( -\infty ;-\dfrac{11}{5} \right )\) ∪ \(\left ( -\dfrac{1}{3};2 \right )\)
+) \(f(x)=0\) với \(x = - \dfrac{{11}}{5}\).
+) \(f(x) > 0\) với \(x ∈ \left ( -\dfrac{11}{5};-\dfrac{1}{3} \right )∪ (2; +∞)\).
LG d
\(f(x) = 4x^2– 1\).
Lời giải chi tiết:
\(f(x) = 4x^2– 1 = (2x - 1)(2x + 1)\).
Ta có:
\(\begin{array}{l}
2x - 1 = 0 \Leftrightarrow x = \dfrac{1}{2}\\
2x + 1 = 0 \Leftrightarrow x = - \dfrac{1}{2}\\
\left( { - \dfrac{1}{2} < \dfrac{1}{2}} \right)
\end{array}\)
Ta lập bảng xét dấu
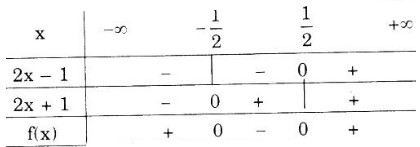
\(f(x) = 0\) với \(x = \pm \dfrac{1}{2}\)
Vậy,
+) \(f(x) < 0\) với \(x ∈ \left ( -\dfrac{1}{2};\dfrac{1}{2} \right )\)
+) \(f(x) > 0\) với \(x ∈ \left ( -\infty ;-\dfrac{1}{2} \right )∪ \left ( \dfrac{1}{2};+\infty \right ).\)
Loigiaihay.com
- Bài 2 trang 94 SGK Đại số 10
- Bài 3 trang 94 SGK Đại số 10
- Câu hỏi 4 trang 92 SGK Đại số 10
- Câu hỏi 3 trang 92 SGK Đại số 10
- Câu hỏi 2 trang 90 SGK Đại số 10
>> Xem thêm